10. Prefix Sum

Prefix Sum, 유명하고 상당히 쉬운 측에 속하는 알고리즘입니다.

물론.. 알고리즘이라 부르기도 조금 민망할 정도로 간단한데.. 활용하기 좋은 방법이라 소개드립니다.

 

---

Prefix Sum

누적합, 구간합이라 불리며 누적합 또는 구간합을 빠르게 구하는 알고리즘입니다.

 

 

Prefix라는 단어를 사전에서 찾아보면 '접두사'라는 뜻을 갖습니다.

접두사라는 용어보다는 단어를 분해해 이해하는 것이 좀 더 와 닿습니다.

pre-
~ 이전의, 미리

fix
고정시키다. 정하다.

 

즉, 미리 어떤 것을 고정시킨다. Sum, 합을 미리 고정시킨다로 받아들이시면 이해가 더 빠를 수도 있겠습니다.

어떻게 고정시키고 어떻게 활용할 것인지 알아봅시다.

 

우선, 어떤 수들의 합을 구하는 문제를 해결해 보겠습니다.

arr = {0, 8, 2, 19, 7, 6, 55, 30 12}

위와 같은 배열이 존재할 때 배열의 수를 모두 합한 결과를 뽑는 코드는 다음과 같습니다.

맨 앞의 0은 prefix sum 코드를 간편하게 만들기 위함입니다. 아래에서 설명드리겠습니다.

public class Main {
    public static void main(String[] args) {
        int[] arr = {0, 8, 2, 19, 7, 6, 55, 30, 12};
        int sum = 0;

        for(int i = 1; i < arr.length; i++) {
            sum += arr[i];
        }

        System.out.println(sum);
    }
}

 

상당히 간단하죠. 이러한 문제는 배열의 원소 수가 많다 해도 O(N)으로 구하는 것이 일반적입니다.

만약 어떤 구간의 합을 구해야 하는 경우는 아래와 같은 코드로 해결할 수 있습니다.

3 구간 (1, 5), (4, 7), (3, 8)의 합 구하기로 가정하겠습니다.

public class Main {

    private static class Section {
        int start;
        int end;

        public Section(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }

    public static void main(String[] args) {
        int[] arr = {0, 8, 2, 19, 7, 6, 55, 30, 12};

        Section[] sections = new Section[3];
        sections[0] = new Section(1, 5);
        sections[1] = new Section(4, 7);
        sections[2] = new Section(3, 8);

        StringBuilder sb = new StringBuilder();

        for(Section sect: sections) {
            int sum = 0;

            for(int i = sect.start; i <= sect.end; i++) {
                sum += arr[i];
            }

            sb.append(sum).append("\n");
        }

        System.out.println(sb.toString());
    }
}

 

결과

(1, 5) 구간합: 42
(4, 7) 구간합: 98
(3, 8) 구간합: 129

해당 코드의 시간 복잡도는 어떻게 될까요? 구간의 수(M), 원소 개수(N)로 잡으면 O(NM)입니다.

즉, N과 M이 10만 이상씩 들어오는 경우엔 시간 초과가 발생하겠죠.

 

하지만, Prefix Sum은 N과 M이 100 만씩 들어온다 해도 시간 내에 해결할 수 있습니다.

 

방식은 간단합니다.

1. 각 인덱스까지 합을 계산해 배열에 저장한다. -> 합을 미리 구함, 고정! (prefix sum 배열 생성)
2. 원하는 구간(i, j)에 대한 결과를 prefix_sum [j] - prefix_sum [i - 1]로 도출해 낸다.

당연하게도 성립된다는 것을 이해하셨다면 코드 부분으로 넘어가시면 됩니다.

 

2번의 식이 어떻게 성립되는지 이해해 봅시다.

우선 사칙 연산은 모두 할 줄 아실 거라 믿고, 40 - 13 = 27이라는 것은 자명합니다.

이 값에 어떤 함수 f(X)를 적용한다면, f(40) - f(13) =? 겠죠.

 

그런데 만약 이 함수가 크기 X의 어떤 배열 p의 인덱스 0 ~ X - 1까지의 합을 반환해주는 함수라고 가정하겠습니다.

그러면 좌변은 f(40) - f(13) 일 때, f(40)은 0 ~ 39번까지의 합이며, f(13)은 0 ~ 12까지 합이죠.

둘을 뺀다는 의미는 (0 ~ 39) - (0 ~ 12)이며, 중복 구간을 제외하면 13 ~ 39까지의 합을 나타냅니다.

중복 구간을 제외시킨다는 것이 핵심입니다.

이렇게 구간 13, 39까지의 누적합을 f(40) - f(13)으로 구할 수 있습니다.

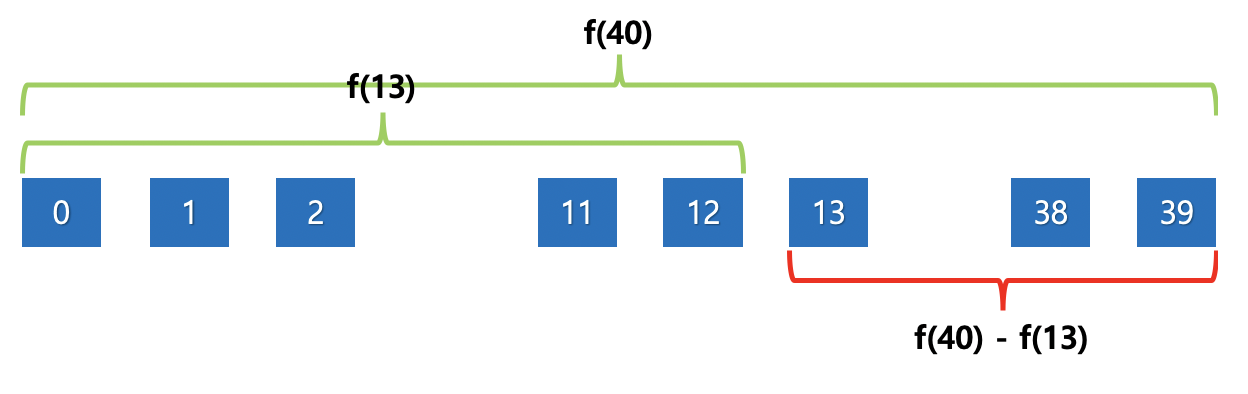
그림 1. 함수 f 결과

 

즉, 미리 i까지의 합, j의 까지의 합을 구해만 둔다면, 구간 (i, j)의 누적합을 O(1)만에 구할 수 있겠습니다.

수식으로 나타내면 아래와 같습니다.

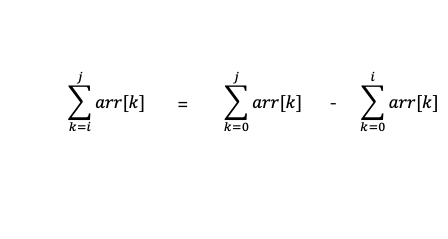
그림 2. prefix sum 수식

 

또한, 함수의 정의가 아래와 같이 바뀌면 처음 40 - 13 = 27이라는 수식도 결국 같은 의미입니다.

f(X)는 어떤 배열 p의 0부터 X까지의 합을 나타낸다. (단, 배열의 값은 모두 1로 채워진 상태)

 

 

이 내용을 이해를 하셨다면, 먼저 prefix sum(합을 미리 고정)하시면 됩니다. 후후

아무튼 같은 이야기를 여러 가지로 변형해서 말씀드렸는데, 실제로 코드는 어떻게 되는지 확인해보겠습니다.

앞에서 예시로든 arr에 적용한다면 sum 배열은 이와 같이 정의됩니다.

sum = {0, 8, 10, 29, 36, 42, 97, 127, 139};

보시는 바와 같이 각 인덱스가 의미하는 것은 'arr [1] ~ arr [i]까지 모든 원소의 합'입니다.

따라서, 구간 3개 중 (1, 5)에 대한 값은 간단히 sum [5]를 출력함으로써 구해낼 수 있습니다. (sum [0] 생략)

또한, 위에서 말씀드린 바와 같이 sum [7] - sum[3], sum[8] - sum[2]로 각각의 구간합을 빠르게 구할 수 있습니다.

sum[7] - sum [4] = 127 - 29 = 98

sum [8] - sum [3] = 139 - 10 = 129

 

솔직히 너무 간단해서 더 이상 말씀드릴만한 건 없네요 ㅎㅎ

코드 보여드리고 마무리하겠습니다.

public class Main {

    private static int[] sum;

    private static class Section {
        int start;
        int end;

        public Section(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }

    public static void main(String[] args) {
        int[] arr = {0, 8, 2, 19, 7, 6, 55, 30, 12};

        sum = new int[arr.length];
        prefixSum(arr);

        Section[] sections = new Section[3];
        sections[0] = new Section(1, 5);
        sections[1] = new Section(4, 7);
        sections[2] = new Section(3, 8);

        StringBuilder sb = new StringBuilder();

        for(Section sect: sections) {
            sb.append(sum[sect.end] - sum[sect.start - 1]).append("\n");
        }

        System.out.println(sb.toString());
    }

    private static void prefixSum(int[] arr) {
        for(int i = 1; i < sum.length; i++) {
            sum[i] = arr[i] + sum[i - 1];
        }
    }
}

결과

그림 3. prefix sum 결과

 

앞서 배열 크기를 하나 더 늘려 0번에 0을 넣는 이유는

• prefix sum 배열 초기화
• 0부터 값을 채우면 sum [sect.end] - sum [sect.start - 1]에서 -1의 값을 접근하는 것

이 두 가지 이유 때문이며, 굳이 0을 안 넣고 코드를 작성하셔도 무방합니다.

코드가 복잡해질수록 조건문이 까다로워지니 그냥 위에 써드린 대로 하시는 것이 가장 편할 듯합니다 ㅎㅎ

그리고, prefix sum은 2차원 배열에서 사용되는 문제도 있으니, 참고하시기 바랍니다.

크게 어렵진 않습니다.

 

 

해당 알고리즘 시간 복잡도는 배열 크기: N, 구간 쿼리: M개 일 때,

prefixSum O(N) + 구간 합 계산 O(1) * 구간 쿼리 O(M) = O(N + M)입니다.

 

해당 알고리즘은 따로 쓰이는 일은 거의 없고.. 다른 개념과 함께 쓰이는 것이 일반적입니다.

물론 간단한 문제라면 prefix sum만 쓰는 경우도 있습니다.

질문은 없으시겠지만.. 하하; 주시면 답변드리겠습니다.

그리고, 2차원 활용 방식에 대한 건 문제로 소개드리도록 하겠습니다.

 

 

 

 

참고 자료

Wikipedia - Prefix Sum