9. Dijkstra (최단 경로 알고리즘)

최단 경로 알고리즘 중 가장 많이, 자주 접할 수 있는 다익스트라 알고리즘에 대해 설명합니다.

 

---

Dijkstra Alogrithm

그래프 내에서 꼭짓점간 최단 경로를 찾는 알고리즘이다.

알고리즘을 고안한 에츠허르 다익스트라의 이름을 따 다익스트라 알고리즘이라 불립니다.

 

 

일반적으론 하나의 노드에서 다른 하나의 노드까지의 최단 경로를 구하는 알고리즘입니다.

파생된 방식으로 1:1 탐색이 아닌, 1:N, N:1, N:M 탐색 방식이 있습니다.

기초는 1:1 방식이나, 하나의 노드에서 다른 모든 노드로 향하는 최단 경로를 찾아 트리를 구성하는 방식 또한 주로 쓰입니다.

사실 1:N 방법이 더 많이 쓰이긴 합니다.

 

우선 자주 쓰일 용어에 대해 살짝 짚고 넘어가겠습니다.

V: Vertex를 의미합니다. Node, 꼭짓점과 동의어로 생각하시면 됩니다.

E: Edge를 의미합니다. 간선, 변과 동의어로 생각하시면 됩니다.

PQ: 우선순위 큐 자료구조입니다. 이건 통용되는 단어는 아니고 제가 편하게 쓰려고..

 

다익스트라를 구현하는 조건은 아래와 같습니다.

1. 다익스트라는 양수 가중치를 가지는 그래프에서만 작동합니다.
2. 부분 경로의 최단 경로의 집합은 전체 경로의 최단 경로(Optimal substructure)라는 정의를 가집니다.
3. 매번 가장 짧은 E를 경로로하는 V를 찾아 탐색합니다.
4. PQ를 사용합니다. 최단 경로이므로 min heap과 같이 오름차순으로 비용이 정렬된 PQ입니다.
5. 배열을 모두 최댓값(INF)으로 초기화한 후 각 노드에 도달할 때 마다 필요했던 최소 비용을 배열의 값으로 갱신합니다.

 

1번의 내용인 음수 가중치가 존재하는 그래프에서 다익스트라로 구현할 경우 목적지에 도착하지 못합니다.

다익스트라의 구현을 살펴보고 이후 이 문제에 대해서 간단하게 짚어보겠습니다.

 

2 ~ 5의 내용은 다익스트라 알고리즘을 구현하며 살펴보겠습니다.

그리고 대상 노드의 갯수에 따라 여러 방법이 있다 말씀드렸지만, 사실상 큰 차이는 없습니다.

시간복잡도는 조금 다르지만요.

 

 

 

우선 아래와 같은 그래프가 존재한다 가정해봅시다.

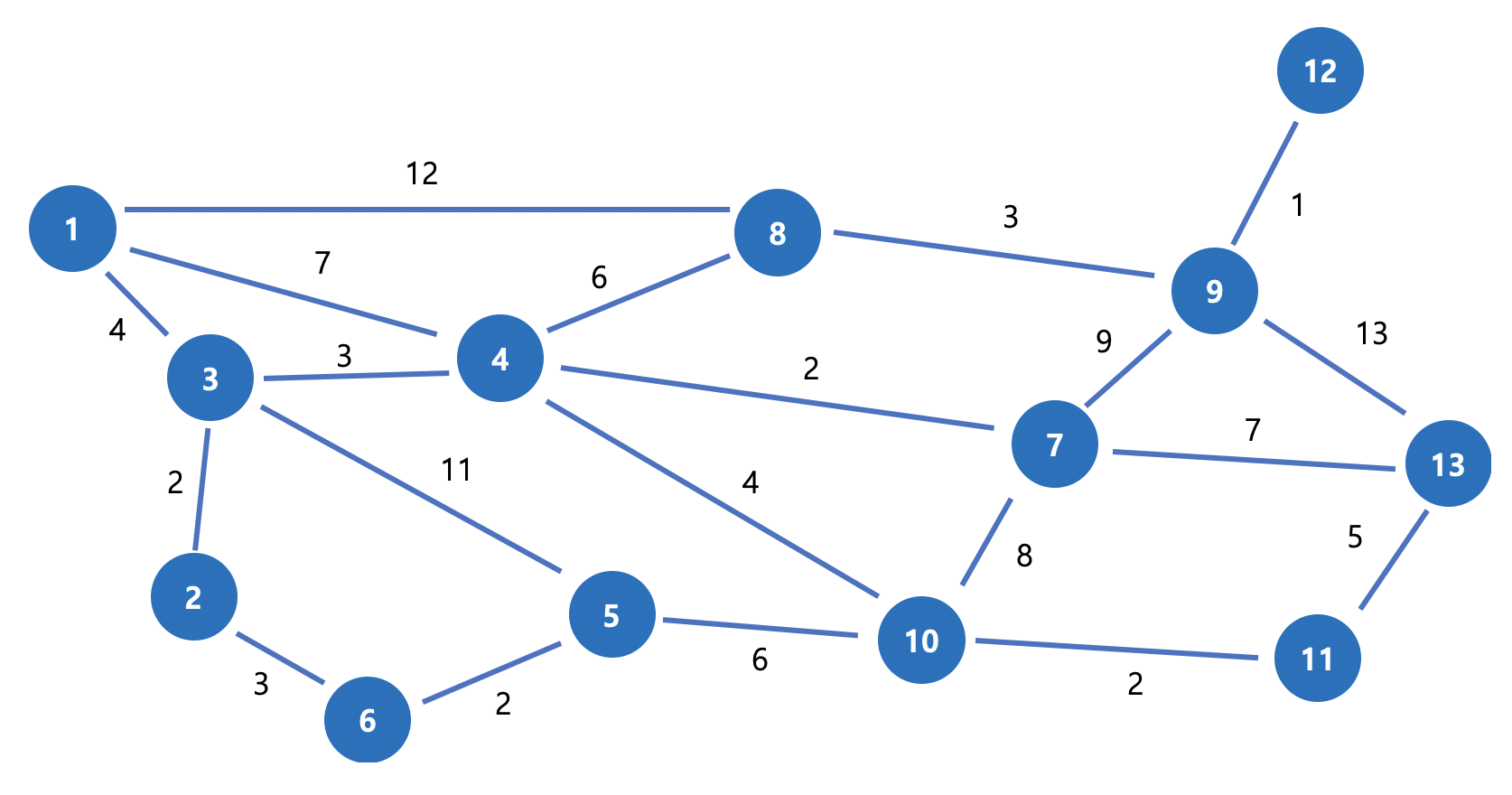
그림 1. 탐색할 그래프

기존에 썼던 그래프인데.. ㅎㅎ;

그냥 쓰기엔 좀 아쉬우니까 이번엔 3번 노드에서 11번 노드까지의 최단 경로를 찾아보겠습니다.

 

최단 경로 후보는 노란색

설정된 최단 경로는 빨간색으로 표기합니다.

또한 시작 노드 3번은 S로 도착 노드 11번은 E로 변경해 표기하겠습니다.

 

 

3번에서 도달할 수 있는 다음 노드를 찾습니다. 1, 2, 4, 5번이 후보 노드가 되겠네요.

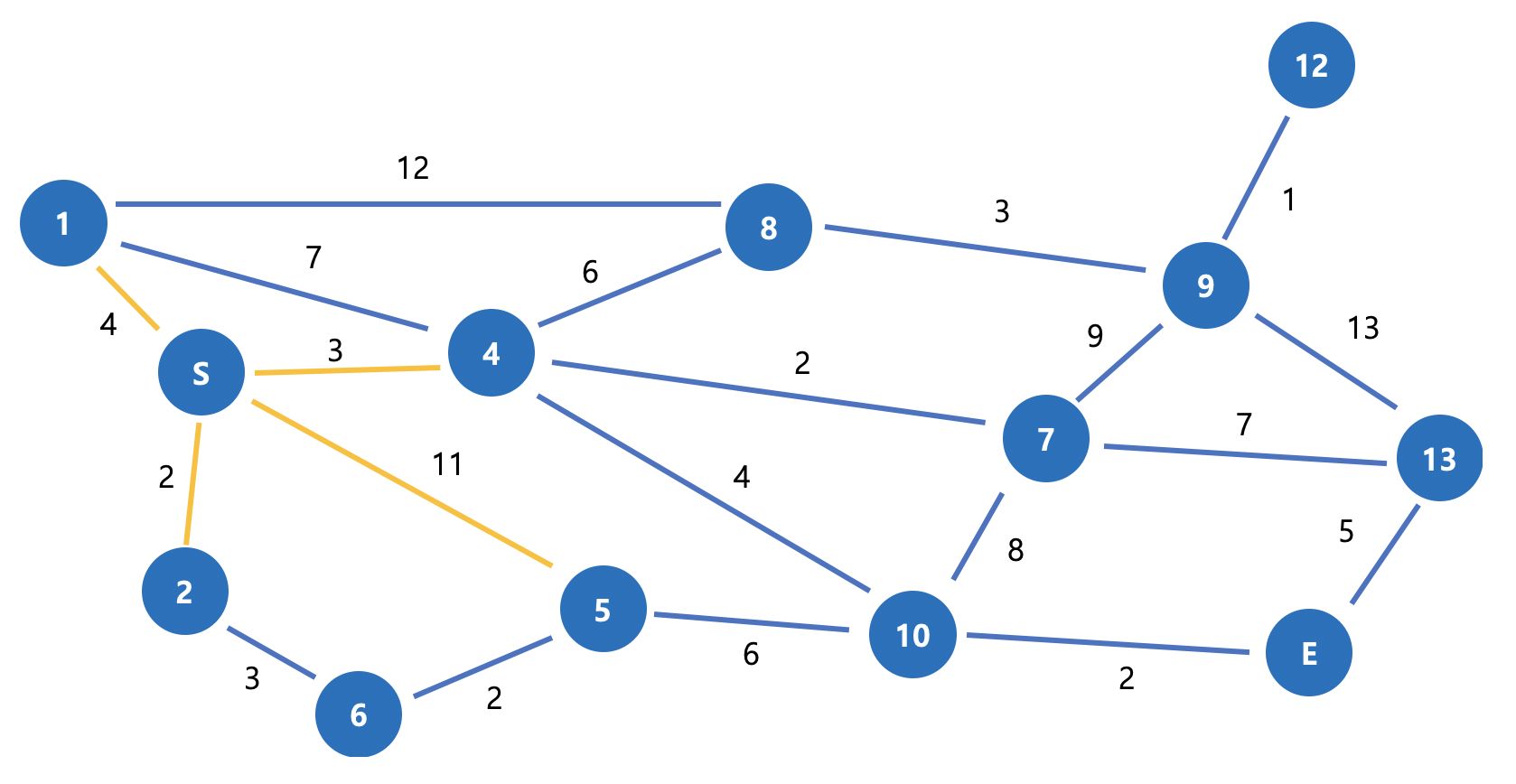
그림 2. 첫번째 후보노드 설정

 

경로가 가장 짧은 노드는 2번입니다. 3 -> 2를 최단 경로로 표시하고 2에서 다시 후보 노드를 찾습니다.

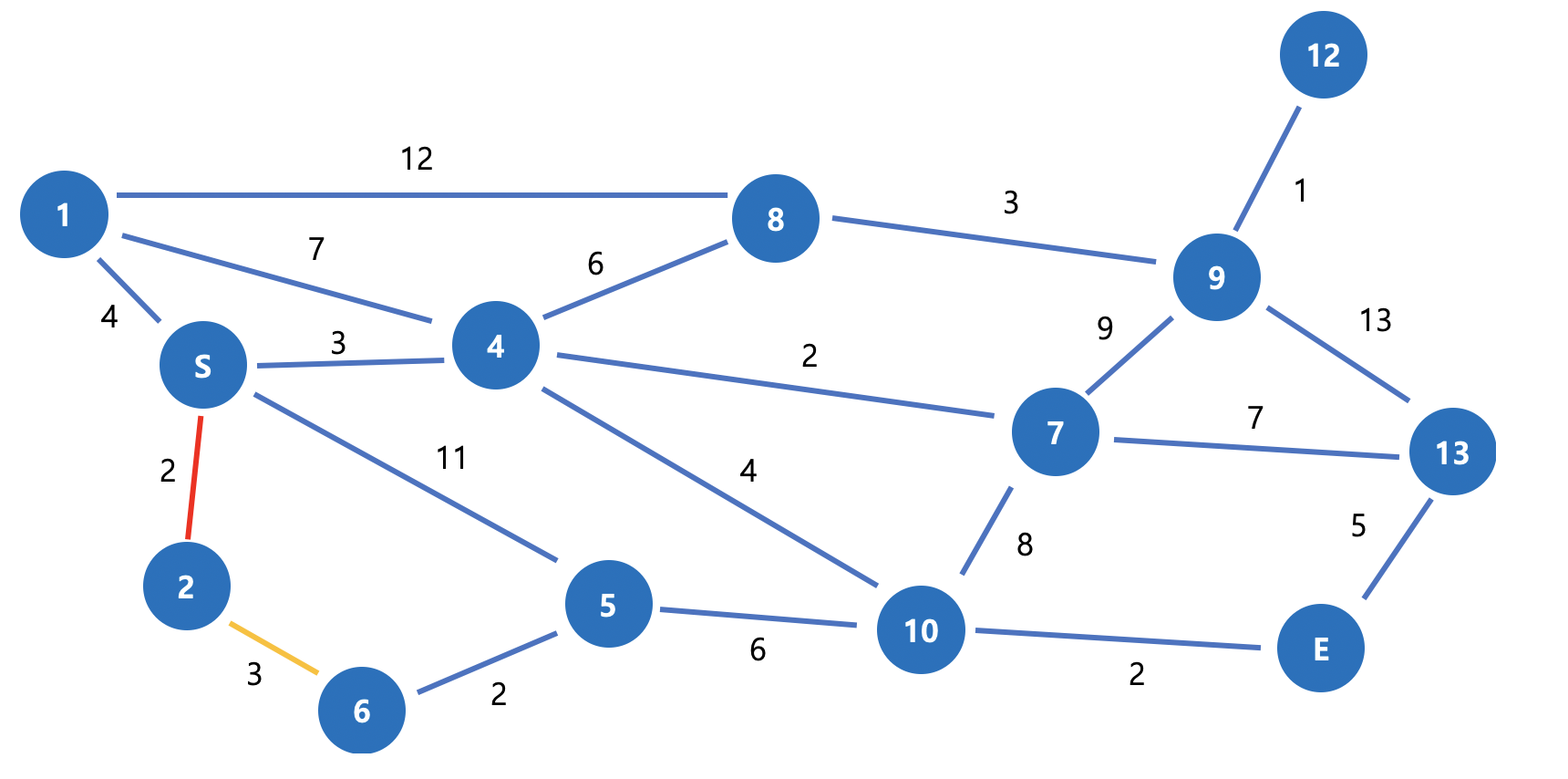
그림 3. 첫번째 최단 경로 설정 및 두번째 후보노드 설정

 

이후로는 반복 작업입니다. 후보노드 중에서 최단경로를 찾고 다시 후보노드를 설정하고..

최종 그래프는 아래와 같습니다.

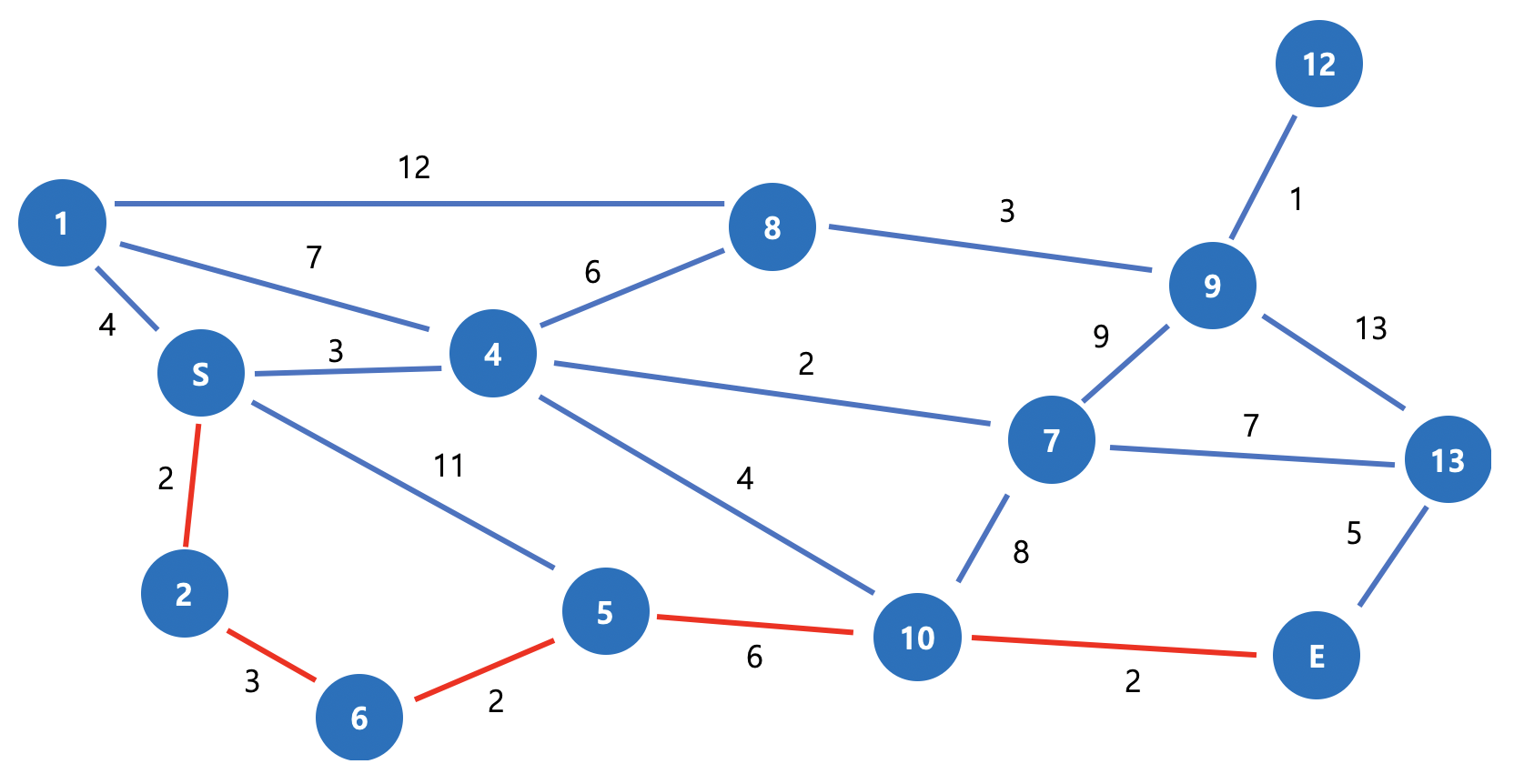
그림 4. 3 -> 11 최단 경로

맞나요? 아니죠... 3 -> 4 -> 10 -> 11 경로가 사실은 최단 경로입니다.

위의 조건 중 3번을 이런식으로 이해하시면 안됩니다.

정확한 의미는 다음에 갈 수 있는 노드들 중 최소 경로를 선택한다는 의미입니다.

따라서, PQ의 작동 방식에 따른 알고리즘의 동작을 잘 이해하셔야합니다.

 

 

이제부터 그 이해를 위해 자세한 동작 방식을 그림과 함께 보여드리겠습니다.

물론 시작할 때 PQ에 3번 노드를 넣는 것은 동일합니다.

 

PQ 원소 구성: [ 다음 노드까지, 해당 경로의 비용 ]

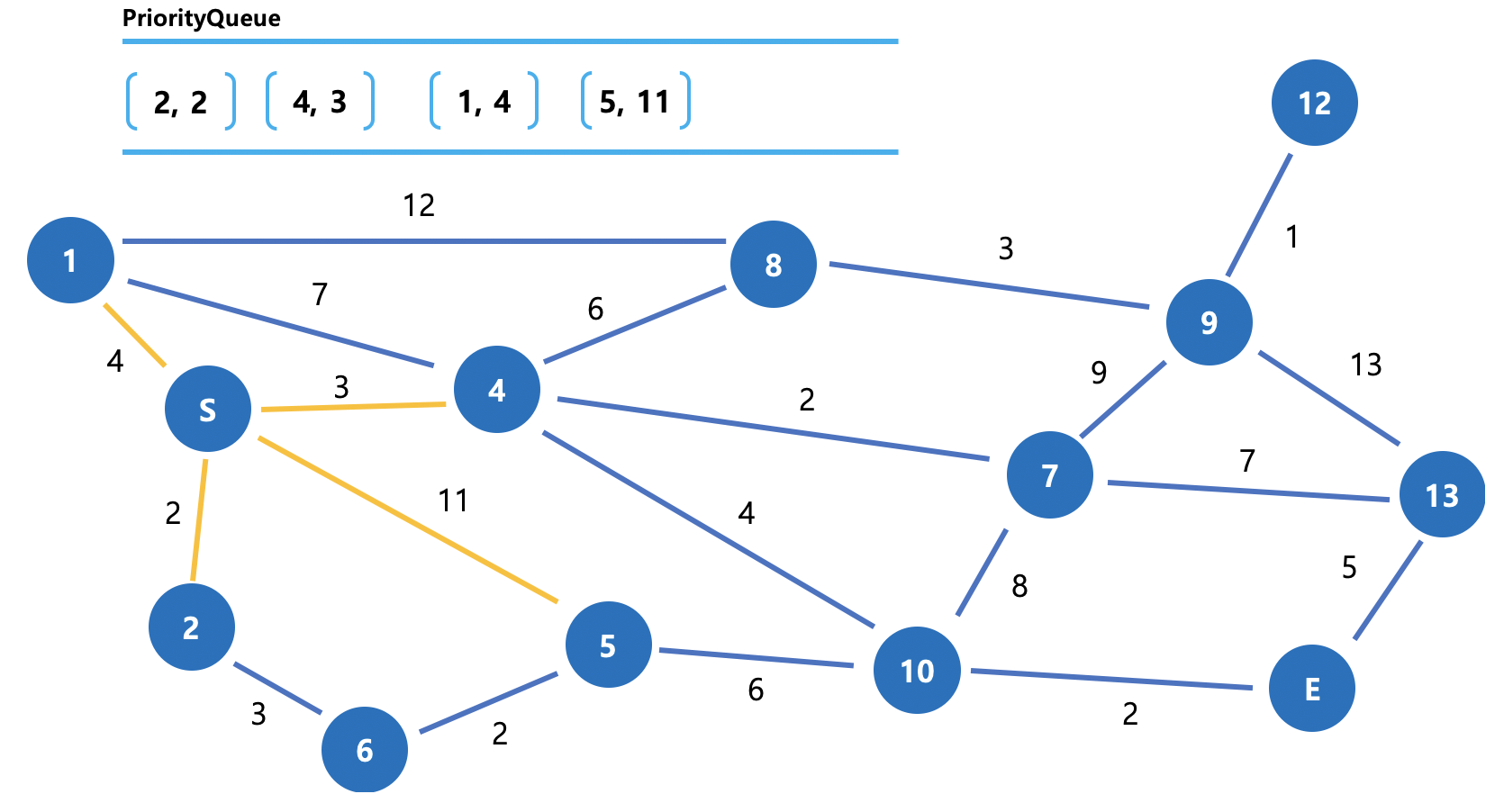
그림 5. 시작점에서 PQ 내부 상태, Dijkstra 동작방식 (1)

우선, 이렇게 PQ에 후보노드를 모두 넣어두고 찾습니다.

물론 PQ 내부에서 E의 비용별 정렬 설정이 되어있기 때문에 비용 순서대로 저장된 모습입니다.

우리는 눈으로 후보 중 최단 경로를 찾았지만, PQ에선 이미 정렬된 상태로 가장 위의 원소를 뽑아내기만 하면 됩니다.

 

 

3 -> 2를 최단경로로 설정하고 다시 다음 후보를 찾는 과정은 아래와 같습니다.

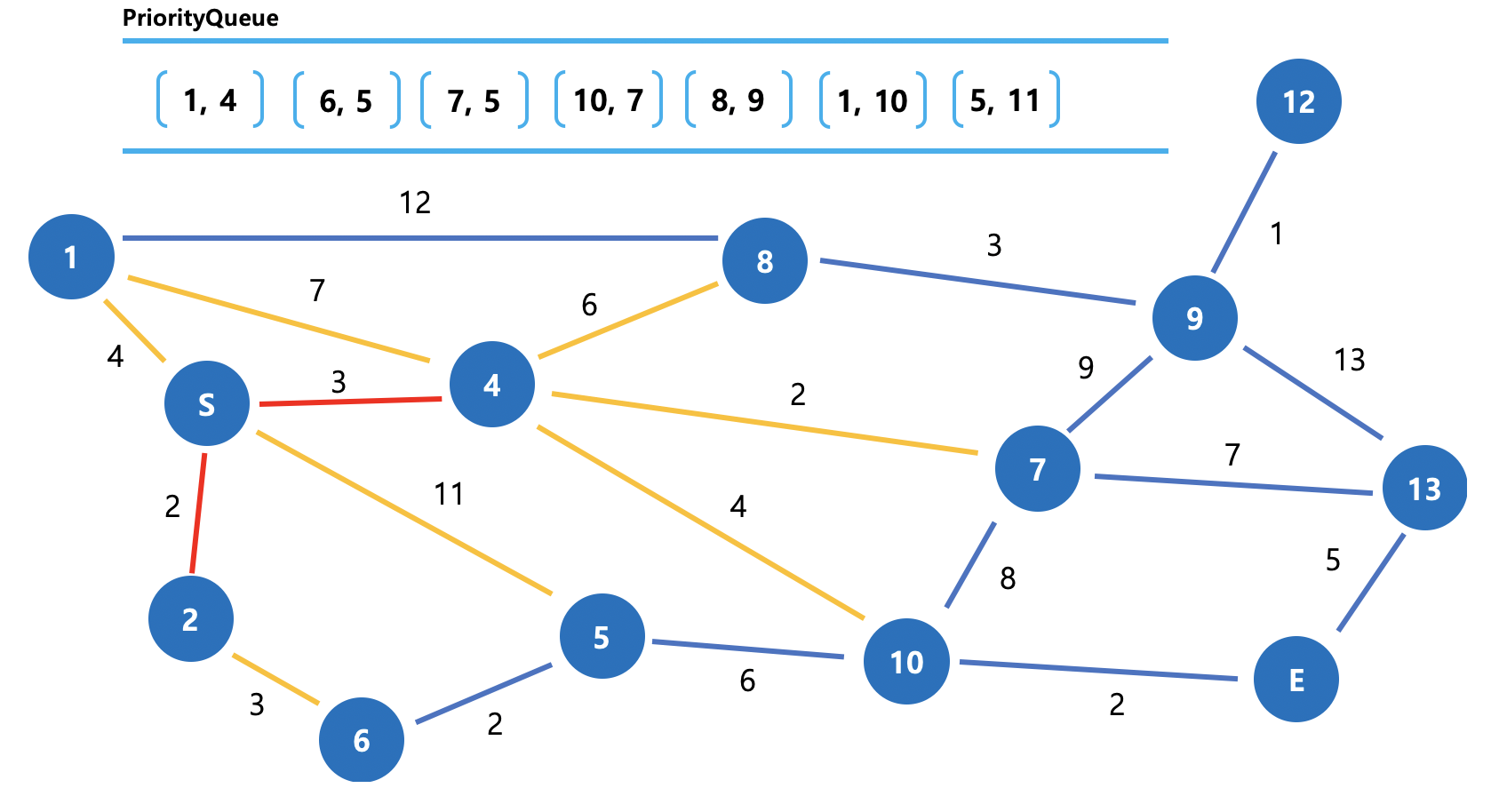
그림 6. 첫번째 최단 경로를 찾은 후 PQ 상태, Dijkstra 동작방식 (2)

이미 파악하신 분도 계시겠으나, 사실은 PQ에 이렇게 저장이 되어있었습니다.

다음엔 2 -> 6을 잇는것이 아닌 3 -> 4을 이어주겠죠.

이를 배열로 본다면 cost[6]의 값을 갱신해 가장 최소 경로를 따라가는 것이 아닌 cost[1]의 값이 갱신됩니다.

3 -> 6 경로는 사실은 3 -> 2까지 포함된 경로이므로 5의 비용이 듭니다.

 

또한 4 -> 1, 4 -> 7, 4 -> 8, 4 -> 10의 경로는 각 경로의 비용에 3 -> 4까지 비용을 포함한 값입니다.

위와 마찬가지로 다음 노드까지의 해당 경로의 비용이니까요.

 

여기서 1로가는 후보 경로가 2가지가 존재하는데요.

4 -> 1, 3 -> 1

아래에서 설명 드리겠지만, 어떤 이유에서 어떻게 고쳐져야 할 지 고민해보시기 바랍니다.

 

 

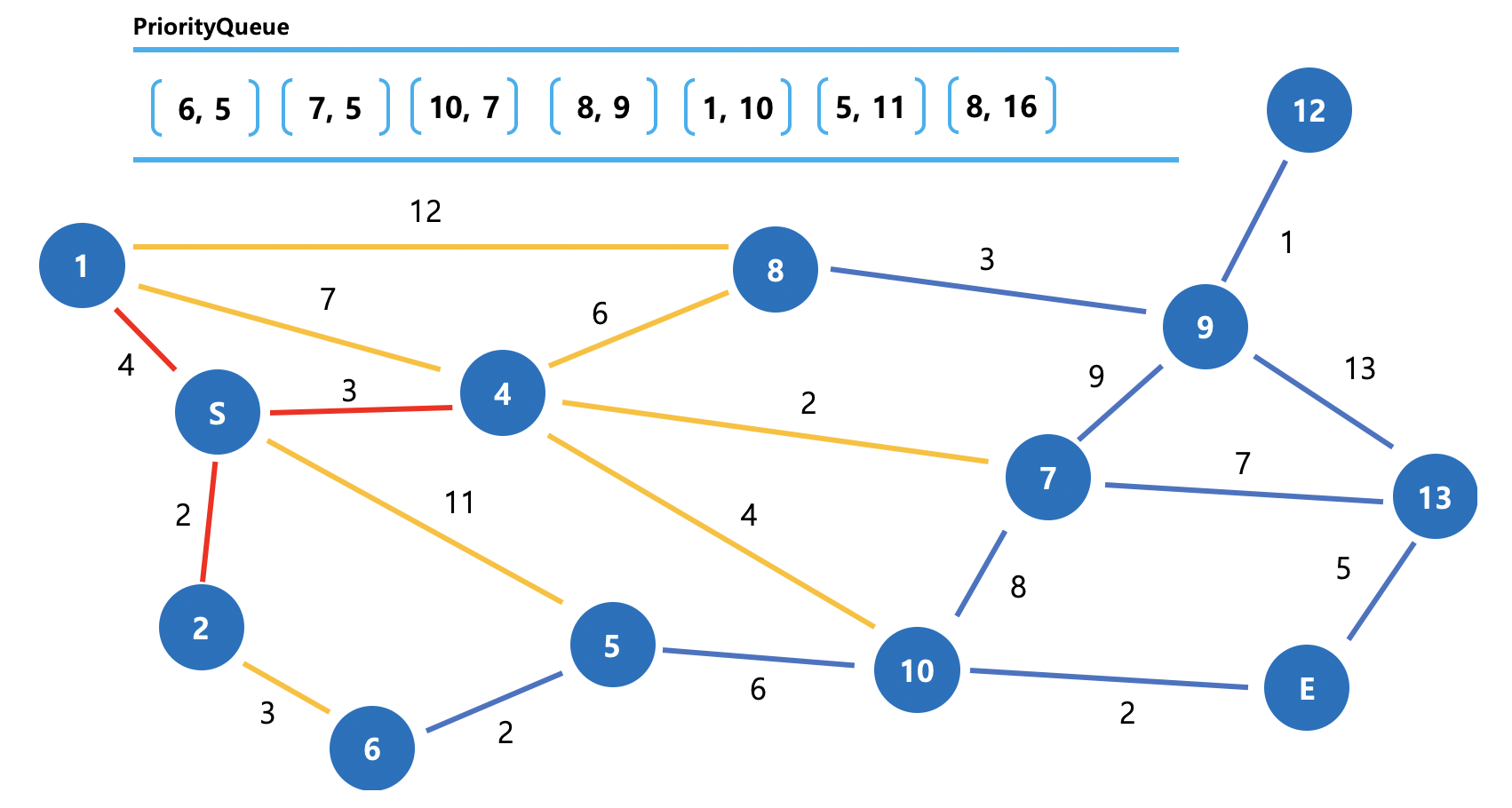
그림 7. Dijkstra 동작방식 (3)

해당 그래프에선 1번으로 가는 비용이 4로 가장 작아 그쪽으로 이동했습니다.

이후 1번 다음 후보노드인 4번에 대한 정보는 PQ에 담지 않는 모습입니다. 왜 그럴까요?

그 이유는 코드를 보시면 좀 더 빠르게 이해가 가실겁니다만,

 

대략적으로 설명드려보면 우린 최단 경로를 찾으려하고 있고 각 경로로 가는 최소 비용을 배열에 저장하죠.

따라서 배열에 들어가있는 최댓값(INF) 또는 더 큰 값을 갱신하며 이동하겠죠.

그러나 이미 갱신되어 저장된 값이 현재 들어오려는 값보다 작다면, 갱신할 필요 없겠죠?

즉, cost[current] <= cost[prev] + egde[cost]인 경우를 의미합니다.

이러한 경우엔 해당 경로의 탐색을 멈춘다는 의미로 PQ에 담지 않습니다.

즉, 이 부분 경로(3 -> 1 -> 4에서 1 -> 4)는 3 -> 4보다 길어 최단 경로의 부분 경로에 사용될 수 없다는 뜻입니다.

즉, 해당 경로는 전체 경로에서 부분 최단 경로가 될 수 없다는 의미를 가집니다. 다익스트라 알고리즘의 정의에도 포함되는 내용입니다.

 

이러한 면에서 위에서 말씀드린 1로가는 두 경로를 살펴봅시다.

3 -> 1 -> 8로 가는 경로도 마찬가지입니다.

결국 3 -> 4 -> 1로 이동하는 [1, 10]은 4가 먼저 탐색되었기에 PQ에 포함은 해야합니다.

하지만, 3 -> 1이 훨씬 짧은 경로기 때문에 이후에 걸러지겠습니다.

즉, 순서상 어쩔 수 없이 들어가 있는 요소입니다. 4가 담기지 않는 이유와는 같지만 걸러지는 방식자체가 다르죠.

 

이후부턴 요소가 많아져 새로 들어오는 원소를 후보색과 같은 노란색으로 표기하겠습니다.

 

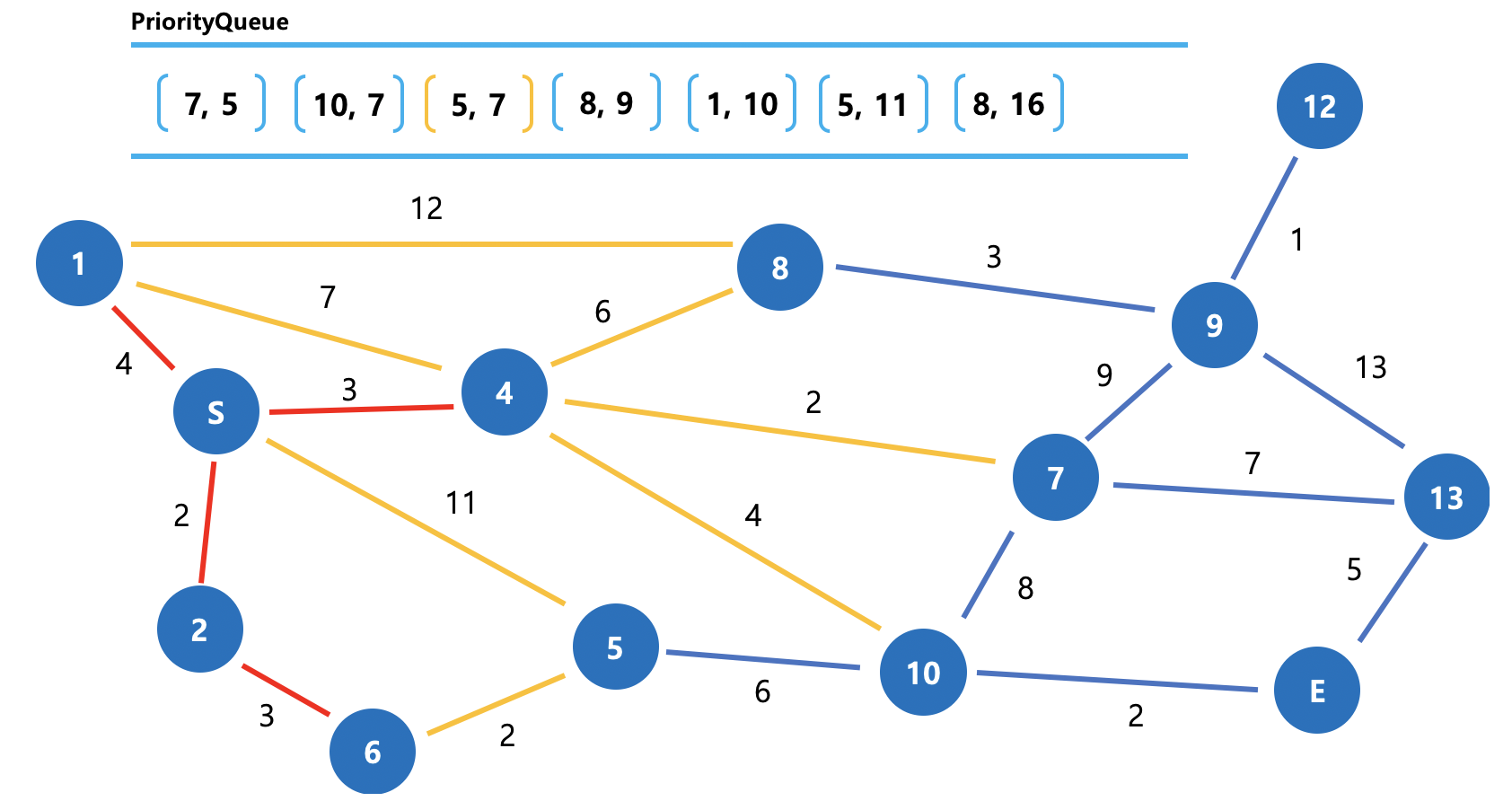
그림 8. Dijkstra 동작방식 (4)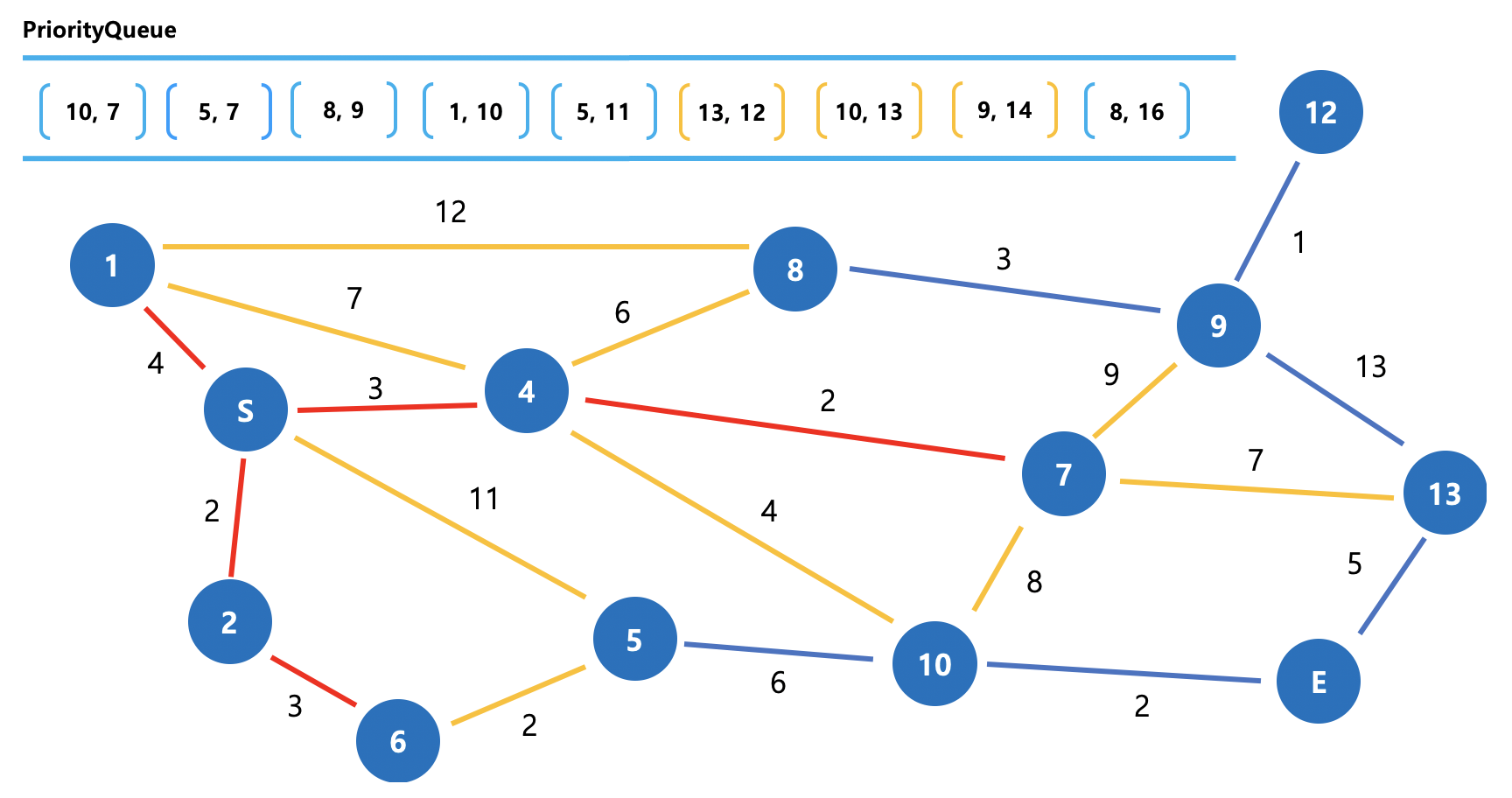

그림 9. Dijkstra 동작방식 (5)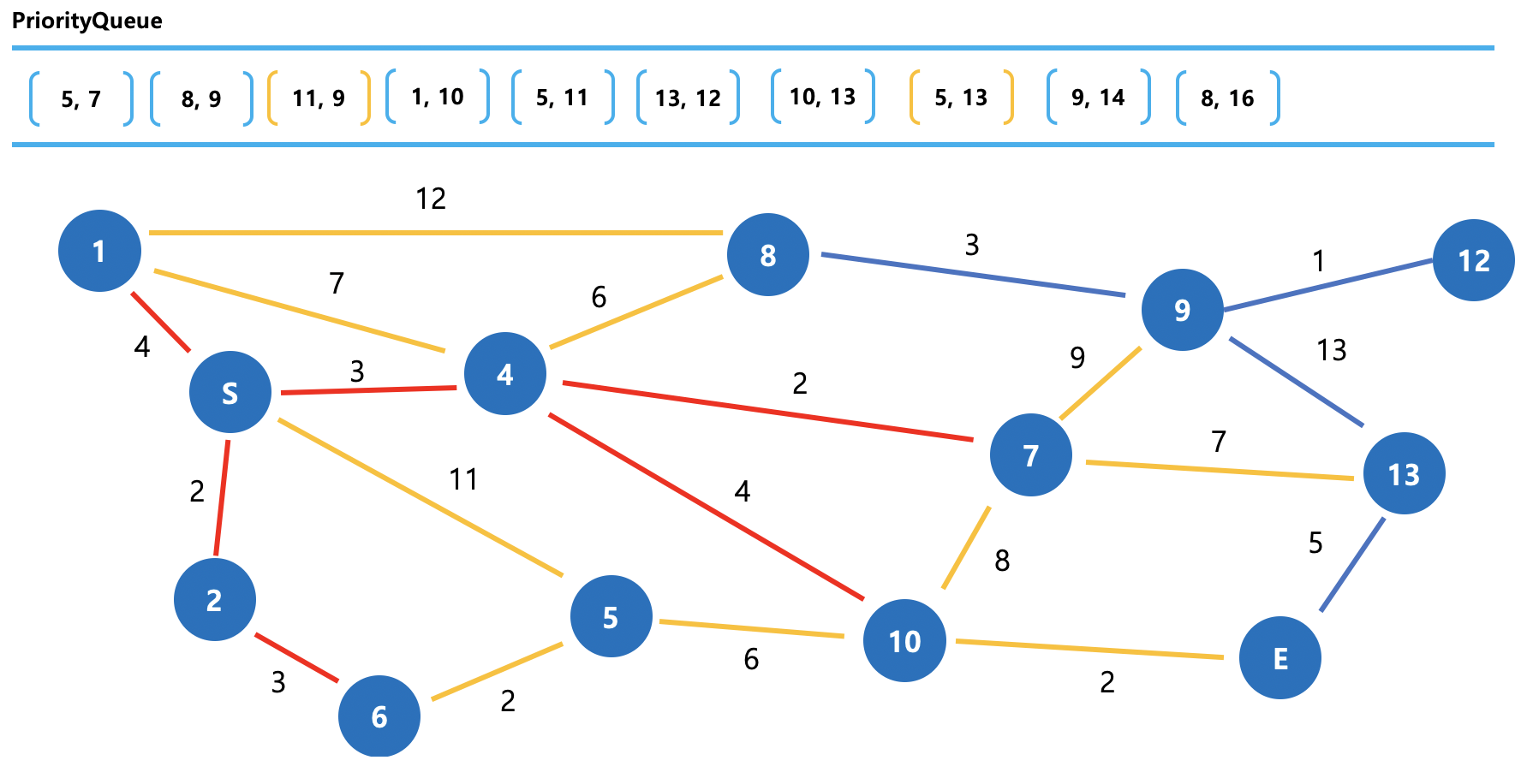

그림 10. Dijkstra 동작방식 (6)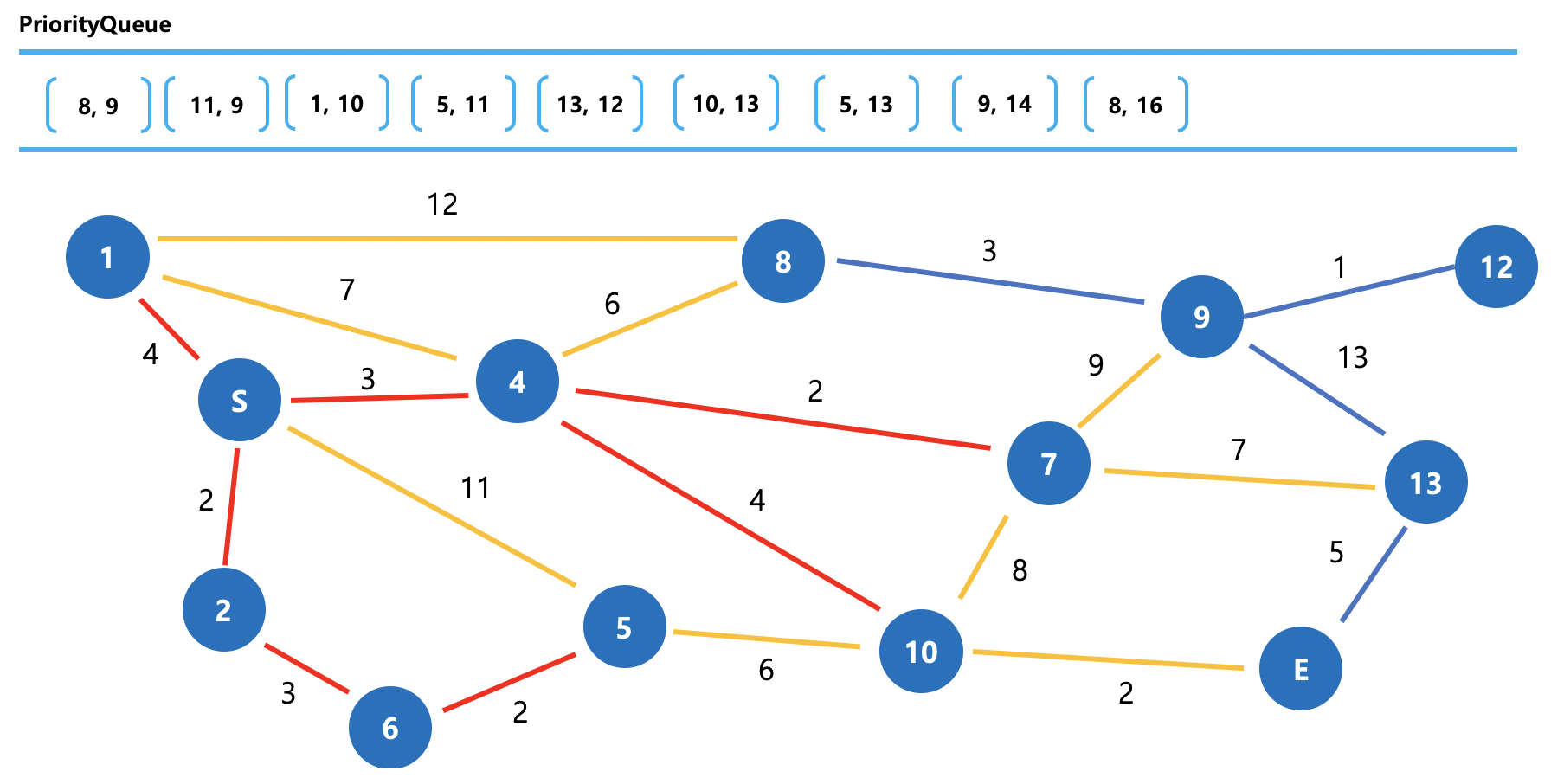

그림 11. Dijkstra 동작방식 (7)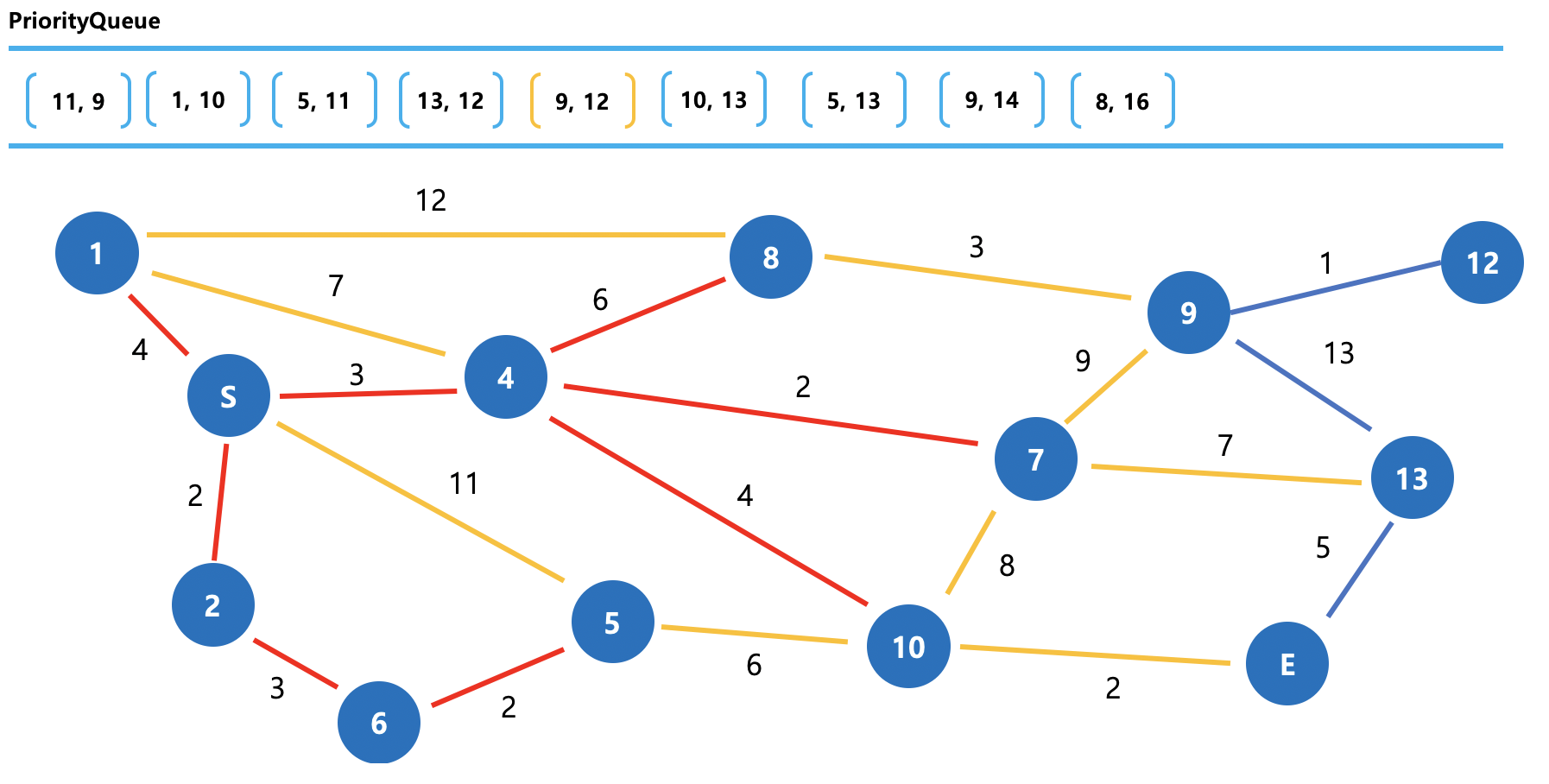

그림 12. Dijkstra 동작방식 (8)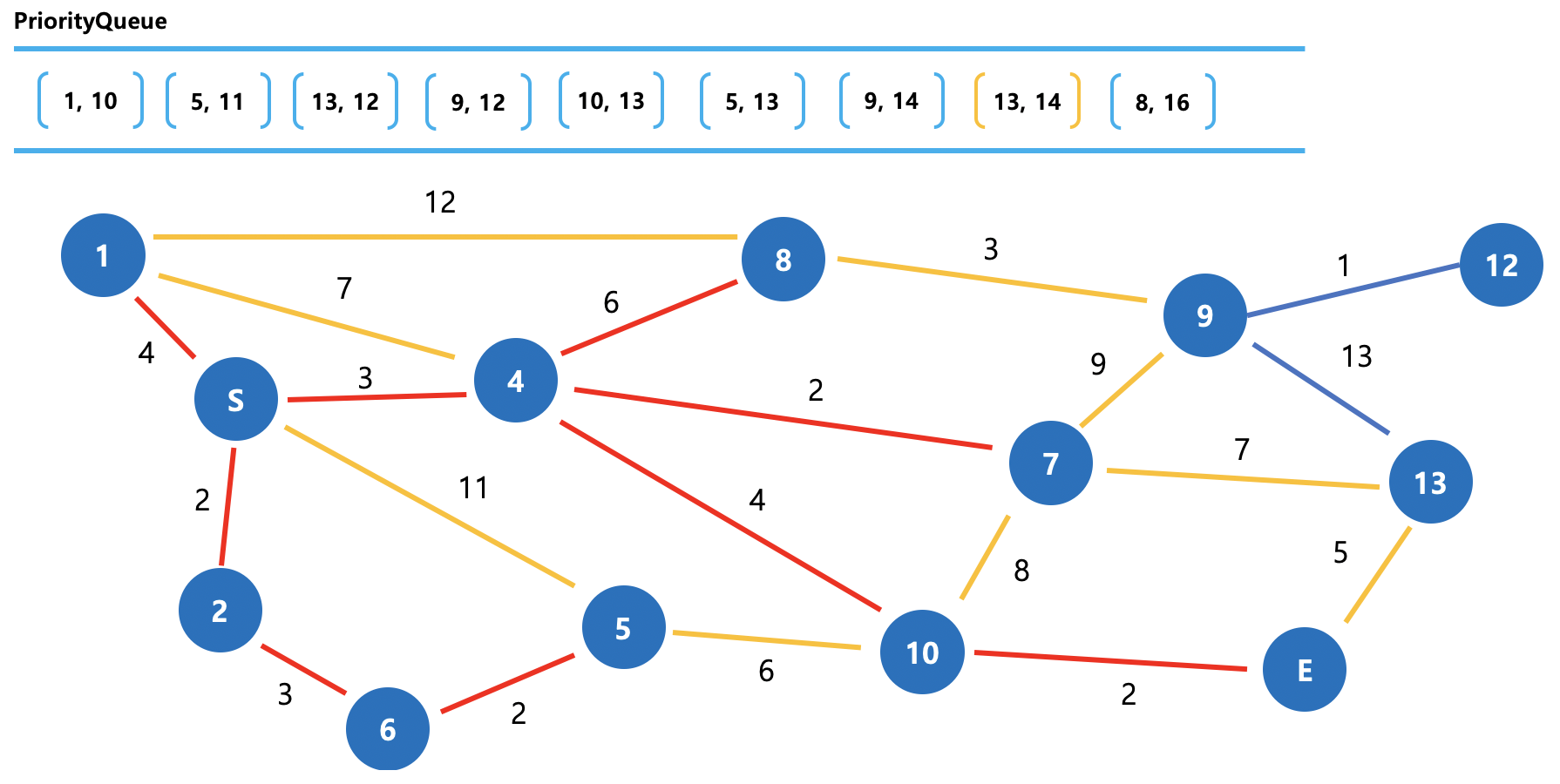

그림 13. Dijkstra 동작방식 (9)

이렇게 앞서 말씀드린 실제 최단 경로인 3 -> 4 -> 10 -> 11 을 찾게되었습니다.

정렬된 PQ내에서 원소에서 가장 경로가 짧은 원소 기준으로 꺼내어 연결한 결과입니다.

 

여기서 E라는 목적지에 도착하자마자 값을 리턴하는 경우 1:1에 대한 최단 경로가 됩니다.

PQ를 모두 비울 때까지 작동시키는 경우 1: N 또는 N: 1 최단 경로를 찾을 수 있습니다.

N: M을 하기 위해선 S를 하나하나 다 지정해주면 되기 때문에 반복문하나와 2차원 배열을 추가하면 되겠습니다.

 

특히, 1: N을 구하는 경우 최단 경로로 이루어진 트리를 만들 수 있습니다.

물론, 시작 노드를 대상으로한 최단 경로입니다.

위 그래프의 최종 모습을 예시로 들면 이렇게 빨간 간선이 트리의 간선이 되겠죠.

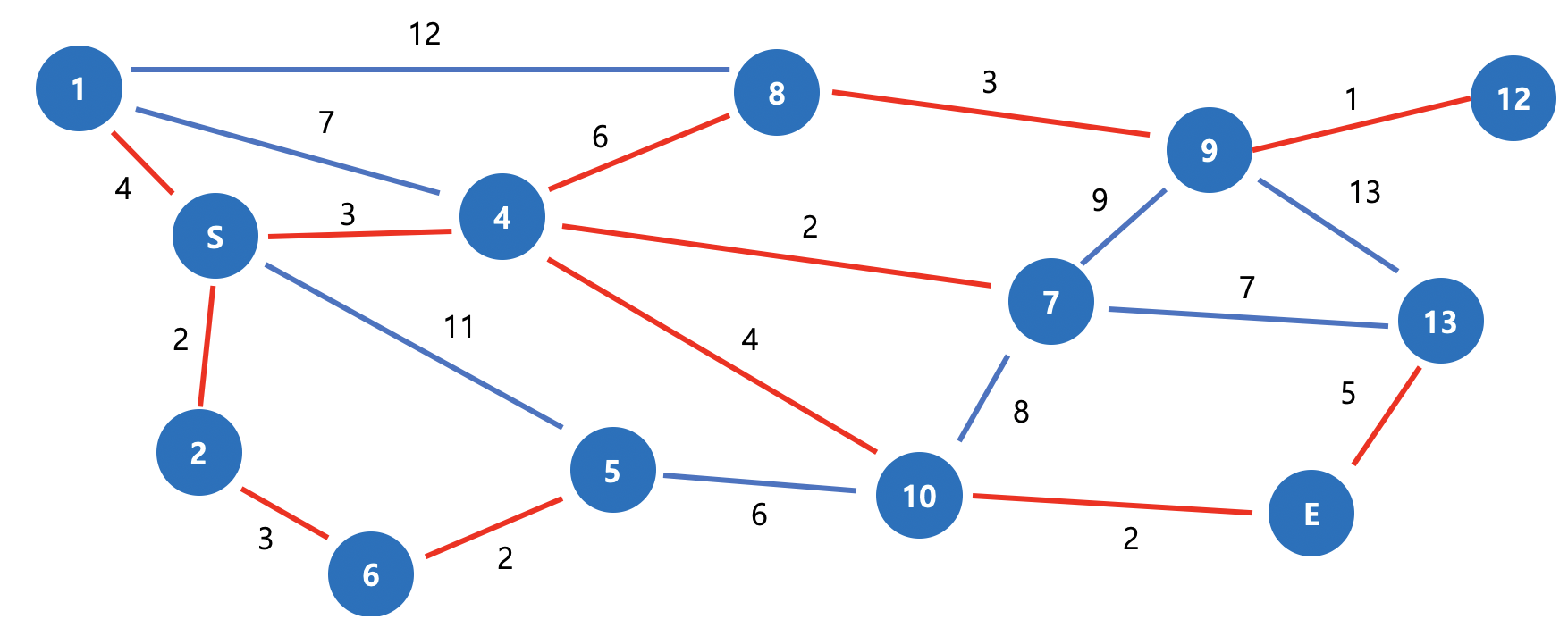
그림 14. 1: N 최종 결과에 의한 트리 생성 (S번 노드 기준)

 

 

여기서 이런 의문점이 드실 수 있습니다.

1:1로 최단 경로를 찾는다 해도 이후에 갱신될 수 있는것 아닌가?, 도착지점에 도달하자마자 리턴해도 되는 것인가?

네, 가장 먼저 도착하는 값이 최적입니다.

 

그래프를 보시고 하나씩 해보셔도 되지만, 다익스트라 알고리즘의 성질을 증명해보면 알 수 있습니다.

의문점을 일반화하고 귀납법으로 보면 아래와 같습니다.

 

부분 문제

어떤 경로 A -> B를 최단 경로라고 가정했을 때, A -> C -> B를 거치는 임의의 정점 C를 지나는 더 최적인 경로가 존재한다.

귀납법 (전체 문제)

전체 경로 A -> .... -> B가 최단 경로라고 가정할 때, 더 최적인 A -> ... -> C -> ... -> B인 경로가 존재한다.

 

부분 문제가 참이라면, 다른 최단 경로가 존재할 수 있기 때문에 바로 리턴해선 안되겠죠.

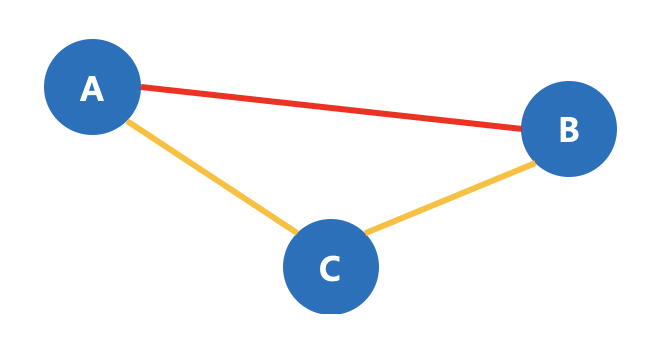
그림 15. 부분 문제

부분 문제를 설명하는 그림은 이와 같습니다.

PQ에서 이미 A -> B가 최소의 값을 가져서 빼내 연결했고, 나머지는 후보로 PQ에 담겨진 상황이죠.

조금만 생각해보시면 이 명제는 거짓임을 알 수 있습니다.

왜냐하면, A -> B보다 최소인 값이 존재 했다면 PQ에서 먼저 빼내 연산이 진행 됐겠죠.

 

정확한 수치로 여러 경우를 봐도 마찬가지입니다.

 

 

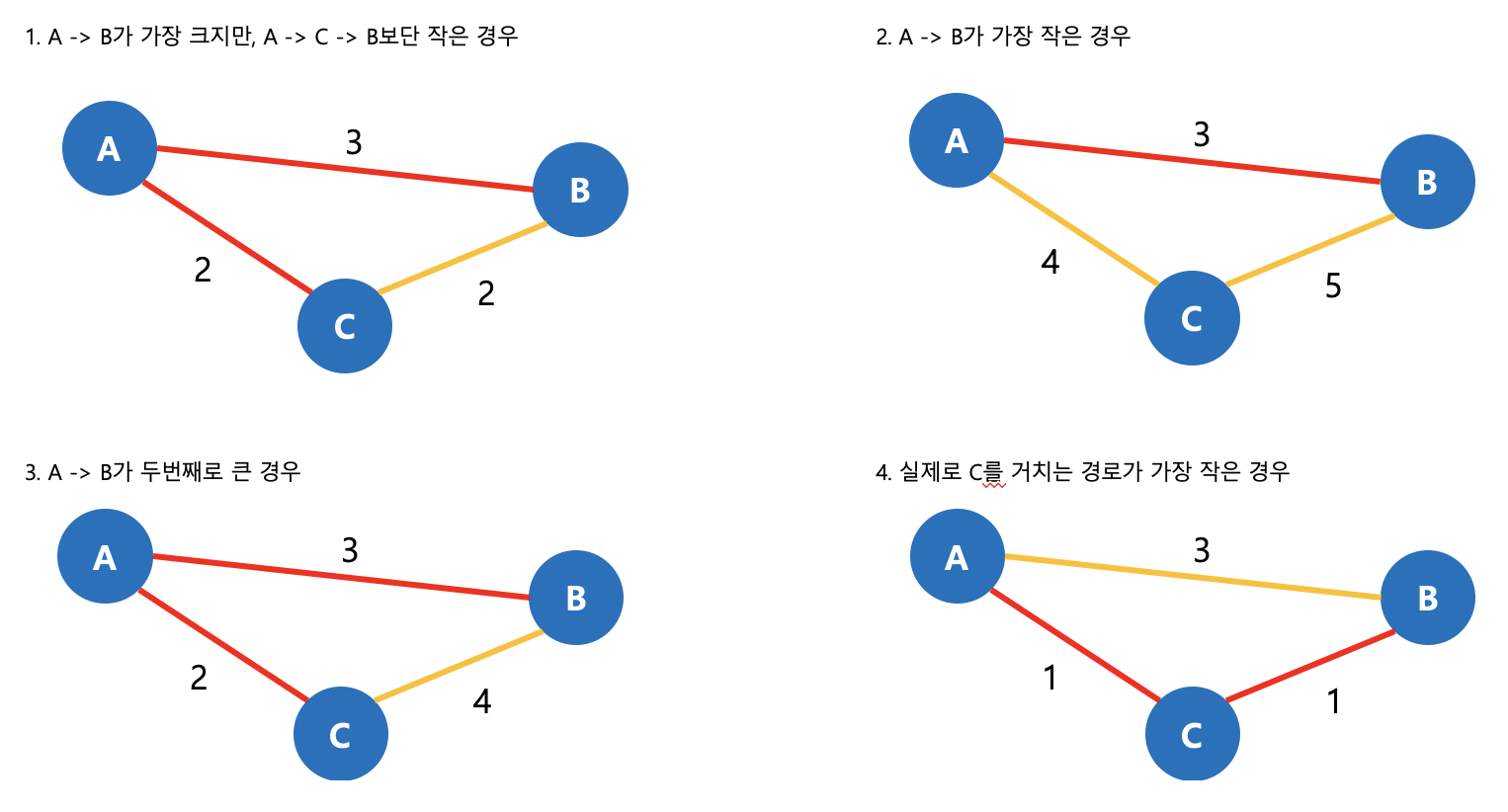
그림 16. 부분 문제 경우의 수

4번의 경우는 이미 A -> B가 최단 경로가 아닌 경우이므로 완전히 다른 경우 입니다.

장황하게 설명을 했는데, 사실 너무 당연한 얘기였습니다.

 

3번의 경우 중간 경로가 여러개라 가정해도(C, D, E ....Z), 최종적으로 A -> B가 가장 짧다면 C, D, E ... Z를 모두 연결하고 마지막에 Z -> B를 연결하는 것이 아닌 PQ에 의해 A -> B가 연결되어버리니 이러한 성질을 만족하게 됩니다.

즉, 두 명제 모두 거짓이므로 최종 목적지에 가장 먼저 도달하는 값이 최적해입니다.

 

구현

이제 코드를 구현하겠습니다.

설명을 양방향 그래프로 했기 때문에 양방향 그래프로 설정하겠습니다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Main {
    private static ArrayList<Node>[] graph;

    private static final String NEW_LINE = "입니다.\n";
    private static final String TO = "에서 ";
    private static final String MIN_COST = "의 최소 비용은 ";
    private static final int INF = Integer.MAX_VALUE;

    private static class Node implements Comparable<Node>{
        int node;
        int cost;

        public Node(int node, int cost) {
            this.node = node;
            this.cost = cost;
        }

        @Override
        public int compareTo(Node n) {
            return this.cost - n.cost;
        }
    }

    /**
     * Main input data
     *
     * line 50 ~ 58: bidirectional graph input
     *
     * @param args
     * @throws Exception
     */
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        graph = new ArrayList[N + 1];
        for(int i = 0; i < graph.length; i++) {
            graph[i] = new ArrayList<>();
        }

        while(M-- > 0) {
            st = new StringTokenizer(br.readLine());
            int node1 = Integer.parseInt(st.nextToken());
            int node2 = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());

            graph[node1].add(new Node(node2, cost));
            graph[node2].add(new Node(node1, cost));
        }

        System.out.println("dijkstraNodeToNode의 결과");
        System.out.println(dijkstraNodeToNode(N, 3, 11));
        System.out.println();
        dijkstraNodeToN(N, 3);
        dijkstraNToM(N);
    }

    /**
     *
     * Node(3) to node(11) the shortest path (1:1)
     *
     * line 91: next.node's cost is not bigger than current.node's cost and the path's cost -> continue
     * That is, this node(next) is already updated by minimum cost
     *
     * @param n
     * @param start
     * @param end
     * @return The shortest path of 3 to 11, if INF, cannot approach
     */
    private static int dijkstraNodeToNode(int n, int start, int end) {
        PriorityQueue<Node> pq = new PriorityQueue<>();

        int[] cost = new int[n + 1];
        Arrays.fill(cost, INF);

        pq.offer(new Node(start, 0));
        cost[start] = 0;

        while(!pq.isEmpty()) {
            Node current = pq.poll();

            for(Node next: graph[current.node]) {
                if(cost[next.node] <= cost[current.node] + next.cost) continue;
                cost[next.node] = cost[current.node] + next.cost;

                if(next.node == end) return cost[next.node];
                pq.offer(new Node(next.node, cost[next.node]));
            }
        }

        return INF;
    }

    /**
     *
     * Node(3) to All the shortest path (1:N)
     *
     * line 132 ~ 138: The shortest path from 3 to All
     *
     * @param n
     * @param start
     */
    private static void dijkstraNodeToN(int n, int start) {
        PriorityQueue<Node> pq = new PriorityQueue<>();

        int[] cost = new int[n + 1];
        Arrays.fill(cost, INF);

        pq.offer(new Node(start, 0));
        cost[start] = 0;

        while(!pq.isEmpty()) {
            Node current = pq.poll();

            for(Node next: graph[current.node]) {
                if(cost[next.node] <= cost[current.node] + next.cost) continue;
                cost[next.node] = cost[current.node] + next.cost;

                pq.offer(new Node(next.node, cost[next.node]));
            }
        }

        StringBuilder sb = new StringBuilder();
        sb.append("dijkstraNodeToN의 결과 \n");
        for(int end = 1; end <= n; end++) {
            sb.append(start).append(TO).append(end).append(MIN_COST).append(cost[end]).append(NEW_LINE);
        }

        System.out.println(sb.toString());
    }

    /**
     *
     * All to All the shortest path (N: M)
     *
     * line 172 ~ 184: The shortest path of from All to All
     *
     * @param n
     */
    private static void dijkstraNToM(int n) {
        int[][] cost = new int[n + 1][n + 1];
        for(int i = 0; i <= n; i++) {
            Arrays.fill(cost[i], INF);
        }

        for(int start = 1; start <= n; start++) {
            PriorityQueue<Node> pq = new PriorityQueue<>();
            pq.offer(new Node(start, 0));
            cost[start][start] = 0;

            while(!pq.isEmpty()) {
                Node current = pq.poll();

                for(Node next: graph[current.node]) {
                    if(cost[start][next.node] <= cost[start][current.node] + next.cost) continue;
                    cost[start][next.node] = cost[start][current.node] + next.cost;

                    pq.offer(new Node(next.node, cost[start][next.node]));
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        sb.append("dijkstraNToM의 결과 \n");
        for(int start = 1; start <= n; start++) {
            sb.append(start).append("에서 다른 노드까지 최소 비용들은 아래와 같습니다. \n");

            for(int end = 1; end <= n; end++) {
                sb.append(end).append("번: ").append(cost[start][end]).append(", ");
            }

            sb.append(NEW_LINE);
        }

        System.out.println(sb.toString());
    }
}

1:1, 1:N, N:M 모두 구현해봤습니다. 기본 설정은 시작 노드는 3, 종료 노드는 11입니다.

결과는 아래와 같습니다.

 

입력

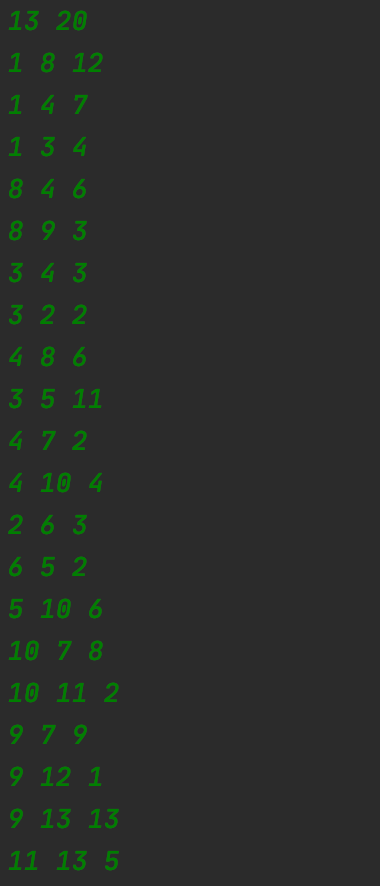
그림 17. 입력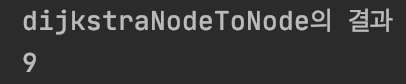

그림 18. 3 -> 11 최소 비용

그림 19. 3 -> All 최소 비용

그림 20. All -> All 최소 비용

코드는 맨 처음 말씀드린 세가지 경우 모두를 구현했습니다.

인접 행렬의 구현도 인접 리스트와 유사하기 때문에 굳이 설명은 생략하겠습니다.

번거롭더라도 하나씩 확인해보시면 어떤 최단 경로는 다른 최단 경로의 부분 경로가 되는 경우도 있습니다.

정의에 따라 결과가 잘 나오네요.

 

코드에서 보시다시피 다음 노드가 PQ에 다시 offer되는 조건은 해당 노드까지의 최단 경로가 갱신된 경우입니다.

이미 최단 경로로 갱신된 값을 다시 탐색할 이유는 없겠죠.

또한, Node To Node에 INF를 리턴하는 경우가 있습니다. PQ가 끝나기도 전에 비는 경우인데요.

목적지 노드까지 경로가 존재하지 않아 최소 비용을 구하지 못하는 경우입니다.

 

 

경로 상 음수가 존재하는 경우만 간략히 보고 시간복잡도 계산 후 마무리하겠습니다.

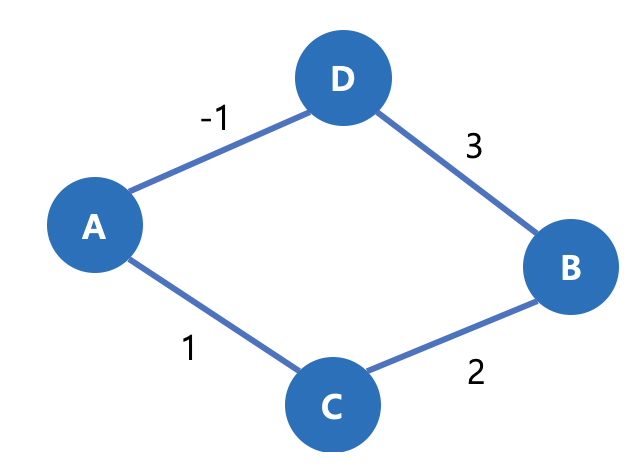
그림 21. 음수 가중치 그래프

A -> B까지 최단 경로를 찾으려 할 때 해당 그래프의 최단 경로는 어떻게 될까요?

 

이제까지 설명을 이해하셨다면, 이 그래프는 다익스트라에서 왜 작동하지 못하는지 아실겁니다.

간단히 말해 무한 루프가 발생해서 프로그램을 빠져나오지 못하기 때문인데요.

 

다익스트라는 다음에 갈 노드가 현재 노드의 비용에서 다음 노드로가는 경로 값을 합한 값

즉, 'cost[next.node] <= cost[current.node] + next.cost' 해당 조건을 확인해 중복 방문 여부를 체크합니다.

하지만 위와 같이 음수 가중치라면 다음으로 갈 노드 값이 항상 크다고 여길 수 밖에 없습니다.

따라서, 계속 값이 갱신되는 현상이 발생하며, 제대로된 탐색이 불가능한 것이죠.

음수 가중치가 존재하면 Bellman-Ford, SPFA, Floyd-Washall 등의 알고리즘을 사용합니다.

관련 내용은 차후 소개드릴까합니다. 특히, Floyd-Washall을 제외하면 음수 사이클이 존재해도 최단 경로를 찾을 수 있습니다.

 

시간 복잡도

변수를 V의 갯수(N), E의 갯수(M)로 잡았으니 시간 복잡도를 이를 기반으로 계산해보겠습니다.

 

우선 1: 1, 1: N의 경우는 같은 복잡도를 가집니다.

PQ에서 노드 V개의 우선순위에 따른 정렬과 이를 기반으로 E개의 경로를 탐색합니다.

따라서 시간 복잡도는 노드 정렬: logV, PQ에서 꺼내 갱신하는 경로 갯수: E -> O (ElogV) 입니다.

 

N: M은 여기에 더 탐색할 노드 M개가 추가되는 것인데, 사실상 N개에서 N개 까지 최단 경로를 구하는 것이겠죠.

O (V) * O (ElogV) = O (VElogV)

 

 

사실 1: 1, 1: N 이런건 그닥 중요하진 않습니다. 그냥 가벼운 응용 정도니까요.

내용 관련해서 잘못된 부분이나 의문점이 있으시면 기록 남겨주시기 바랍니다. 감사합니다.

 

 

 

 

 

 

참고 자료

Wikipedia - Dijkstra Algorithm (Korean)