8. Huffman's Code (허프만 부호화)

막상 찾아보니 알아두면 좋을 것 같아서 후다닥 정리하고 써봅니다.

우선 위키의 정의를 살펴보겠습니다.

 

---

Huffman's Code

전산학과 정보 이론에서 허프먼 부호화(Huffman coding)는 무손실 압축에 쓰이는 엔트로피 부호화의 일종으로, 데이터 문자의 등장 빈도에 따라서 다른 길이의 부호를 사용하는 알고리즘이다. 1952년 당시 박사과정 학생이던 데이비드 허프먼이 《A Method for the Construction of Minimum-Redundancy Codes》란 제목의 논문으로 처음 발표했다.

(출처 wiki)

 

박사 과정은 역시 넘4..

 

생소한 단어가 좀 있는데, 알고 보면 간단한 개념입니다.

우선 엔트로피 부호화는 '심볼이 나올 확률에 따라 심볼을 나타내는 코드의 길이를 달리하는 부호화 방법'입니다.

-> 즉, 빈도수에 따라 어떻게 부호화할지 결정한다. 이렇게 이해하시면 되겠습니다.

 

허프만 코드를 통해 보여드리면 이해가 빠를 테니 따로 예시는 들지 않겠습니다.

정의를 보니 지난 포스팅에서 제가 썼던 말과 같이 데이터 압축이 주 목적인 것으로 보입니다.

 

이 정도만 이해하고 허프만 코드가 어떻게 이루어지는지 알아보겠습니다.

 

 

과정 또한 위키에 잘 나와있습니다.

이 과정을 그림으로 표현하며 따라가 보겠습니다.

 

 

허프먼 알고리즘은 입력 기호를 리프 노드로 하는 이진트리를 만들어서 접두 부호를 만들어 내는 알고리즘이다.

이진트리를 이용해 만든다는 점을 주목해주세요.

접두 부호를 만드는 과정에선 접두부 규칙을 지켜야 합니다.

• 각 문자에 부여된 이진 코드가 다른 문자에 부여된 이진 코드의 접두부가 되지 않는 코드

즉 데이터 X=1101로 설정했다면, Y는 1, 11, 110, 1101의 데이터를 가질 수 없다는 뜻입니다.

(트리 생성 시 이를 주의해서 구성해주셔야 합니다.)

 

 

 

예시문

'afdegasagaggheegff'

 

우선 허프만 코드를 쓰지 않는 경우부터 살펴보겠습니다.

예시문에 포함된 7가지의 알파벳 (a, d, e, f, g, h, s)을 ASCII 기반 데이터로 변환해보겠습니다.

ASCII는 고정 7비트의 크기(0 ~ 127)를 갖습니다.

Alphabet	Frequency	ASCII / Binary
a	4	97 / 1100001
d	1	100 / 1100100
e	3	101 / 1100101
f	3	102 / 1100110
g	5	103 / 1100111
h	1	104 / 1101000
s	1	115 / 1110011

이렇게 정리된 경우 총 3개의 비트를 사용합니다.

총 (4 + 1 + 3 + 3 + 5 + 1 + 1) * 7 = 126 비트가 필요합니다.

가변길이 코드인 허프만 코드를 이용하면 얼마나 압축할 수 있는지 보겠습니다.

 

 

초기화 단계

모든 기호를 출현 빈도수에 따라 나열한다.

Alphabet	Frequency
g	5
a	4
f	3
e	3
d	1
h	1
s	1

 

나열된 데이터를 각각의 리프 노드로 구성해보면 아래와 같습니다.

각 노드의 값은 해당 데이터의 빈도수를 나타냅니다. (내림 차순으로 정렬합니다.)

이 순서로 노드를 고정하고, 트리를 구성할 수 있도록 의도합시다.

 

그림 1. 초기화

다음부턴 반복적인 작업입니다. wiki의 설명을 어떻게든 알아볼 수 있게 정리하면 대략 이런 내용입니다.

 

반복 단계

트리는 상향식으로 구성됩니다.

• 빈도수가 가장 작은 두 개의 노드를 선택해 부모 노드를 생성합니다. (부모 노드의 값은 각 자식 노드 값의 합)
• 단 노드의 값이 큰 부분 트리를 왼쪽에 위치시킵니다.
• 또한 부모 노드 생성 시 왼쪽 노드의 간선에는 0을 오른쪽 노드 간선에는 1을 할당합니다.
• 위의 과정을 노드가 하나 남을 때까지 반복합니다.

이를 그림으로 나타내면 아래와 같습니다.

그림 2. 빈도수가 가장 작은 두 노드 연결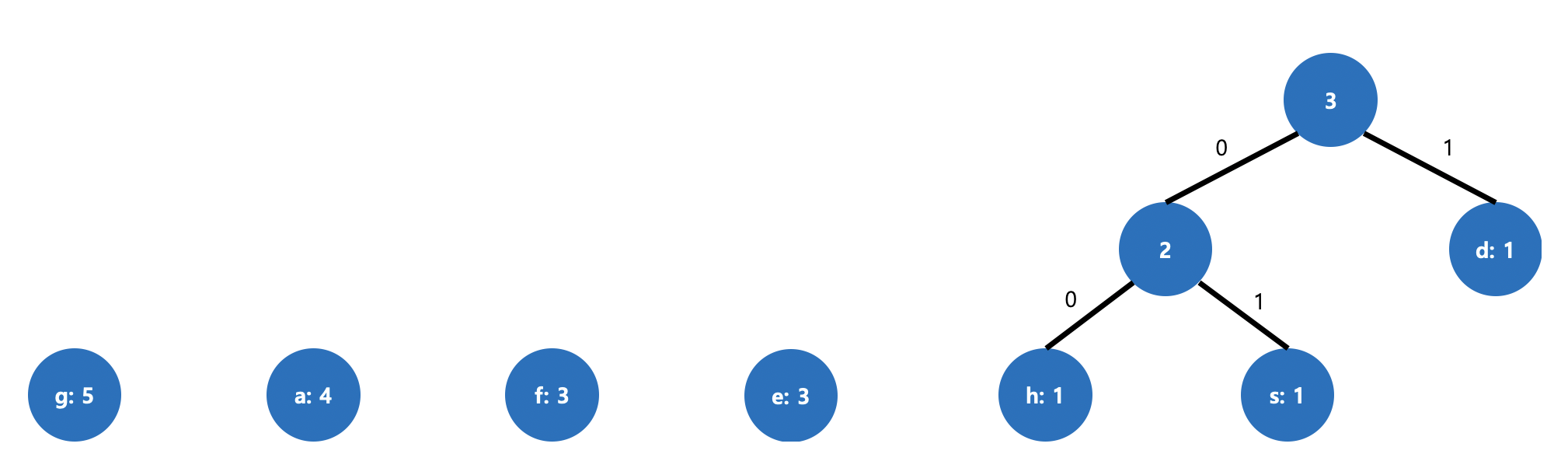

그림 3. 다음 작은 두 노드 연결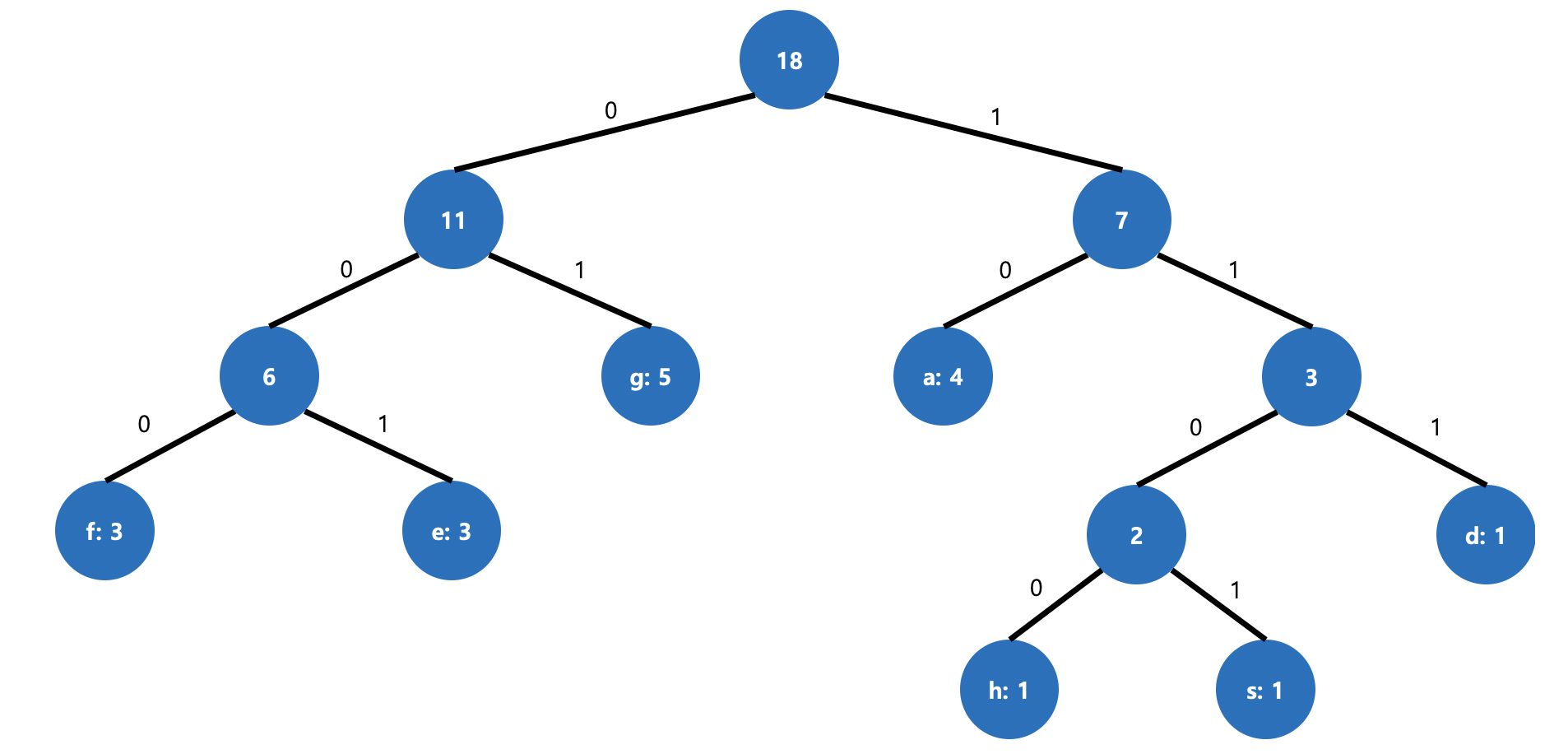

그림 4. 최종 트리

---

이렇게 트리를 완성할 수 있습니다.

이를 표로 정리하면 아래와 같습니다.

Alphabet	Frequency	Huffman code
g	5	01
a	4	10
f	3	000
e	3	001
d	1	111
h	1	1100
s	1	1101

정리된 데이터로 계산된 총 크기는 (5 * 2) + (4 * 2) + (3 * 3) + (3 * 3) + (1 * 3) + (1 * 4) + (1 * 4) = 47 비트입니다.

 

같은 방식으로 다르게 진행해도 같은 결과를 기대할 수 있습니다.

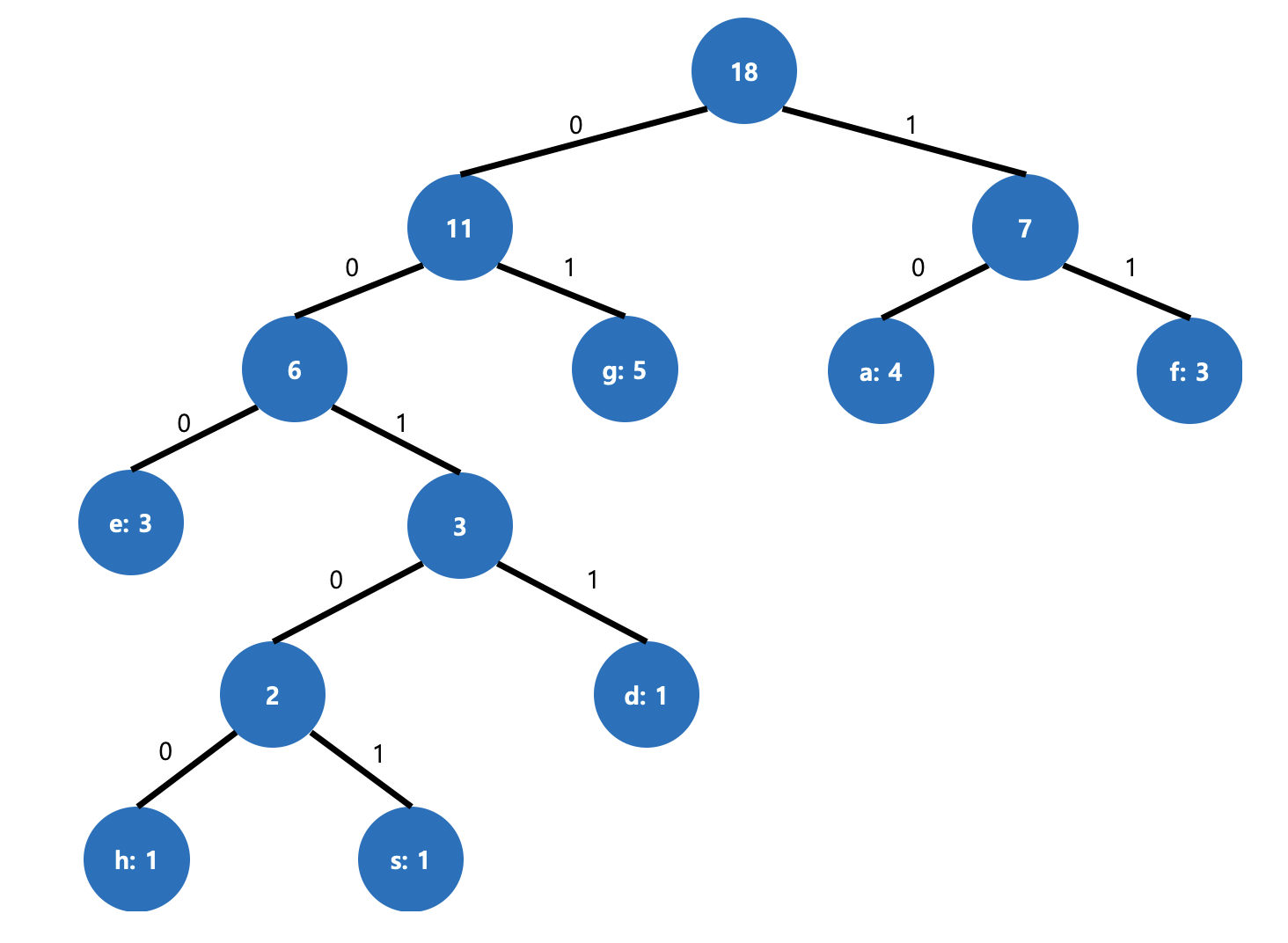
그림 5. 다른 구조 같은 결과

Alphabet	Frequency	Huffman code
g	5	01
a	4	10
f	3	11
e	3	000
d	1	0011
h	1	00100
s	1	00101

 

해당 트리 또한, (5 * 2) + (4 * 2) + (3 * 2) + (3 * 3) + (1 * 4) + (1 * 5) + (1 * 5) = 47 비트로 동일합니다.

결론적으로 처음 봤던 ASCII code에 비해 훨씬 많이 감소했네요. 또한, 접두부 규칙이 잘 적용되어있구요.

누적되는 중복 데이터가 많을수록 더 많은 압축을 기대할 수 있을 것 같습니다.

 

부호화 과정의 시간 복잡도는 문자열의 길이: N, 탐색된 중복 없는 각 문자의 개수: N'으로 본다면,

전체 문자열 탐색: N + 탐색된 문자열 정렬: logN' + 트리 생성: N'logN' = O(N + N'logN') 정도로 나오겠습니다.

N과 N'logN' 중 큰 값이 기준 시간이 되겠네요.

 

어디선가 쓰일만한 구조인 것 같긴 합니다만, 분명 한계는 존재합니다.

 

허프먼 부호화가 항상 최적의 접두 부호를 만들어 내기는 하지만, 접두 부호가 아닌 다른 종류의 부호가 더 효율적일 수도 있다. 예를 들어 여러 문자를 하나의 부호로 묶어 표현할 수 있는 산술 부호화나 LZW 등이 허프먼 부호보다 효율적인 경우가 많으며, 이것은 대부분 하나의 기호를 정수 개의 길이를 가진 부호로서 표현하도록 되어 있는 한계에서 기인한다.

(출처: wiki)

 

또한, 압축된 데이터를 복호화하는 과정에서 필요한 정보는 따로 유지되어야 할 수 있으니 그런 점도 한계가 될 수 있겠네요.

 

제 머리가 따라갈 수 있다면 산술 부호화, LZW도 정리할 수 있었으면 좋겠네요.ㅎㅎ

아 시간 나면 관련 코드도 작성해서 올려보겠습니다.

 

 

관련된 의견, 질문, 피드백 환영합니다.

남겨주시면 같이 고민해보고 보완해보도록 하겠습니다. 감사합니다.