1 - 3. 공유기 설치

백준 2110번: 공유기 설치

2110번: 공유기 설치

 

사실 이 문제는 푼지 좀 오래 되었는데, 완전 같은 문제를 최근에 풀어서 공유합니다.

 

문제는 대충보자면, 한정된 공유기 개수를 가지고 많은 집에서 사용할 수 있도록 적절한 위치에 놓고싶다~ 입니다.

문제에 나오는 도현이는 상당히 선한 사람이면서도, 개발자다운 면모를 갖고 있는 듯 하네요. 멋있습니다.

 

멋있는 도현이를 위해서 저희가 대신 고민해 주도록해요.

 

물론 저 같이 실력은 조잡한데 단지 문제를 많이 푼 사람의 경우에도 어떤 문젠지 단번에 파악은 합니다. ㅎㅎ

하지만, 방심하다 줘터지는게 일상이니, 문제에 나오는 조건들을 잘 따져보고 여러가지 경우의 수를 생각해보죠.

 

 

조건

집의 좌표 (N개, 중복 없음)

공유기 개수(C개, 2 ~ N)

C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로

각 집에는 공유기를 단 한 대 설치가능

 

접근

조건을 보니 아래 두가지가 신경 쓰입니다. 엄청나게..!!

C개의 공유기 / 가장 인접한 두 공유기 사이의 거리

신경 안 쓰이시는 분들은 문제 한번 더 읽고 오세요.

신경이 쓰이니 뭔가 알아내야하겠죠..? 이 두 조건 사이에 어떤 관계가 있을까요?

 

우선, 공유기를 가장 최대로 배치하기 위해선 가장 왼쪽 집과 오른쪽 집 2군데 설치하면 됩니다.

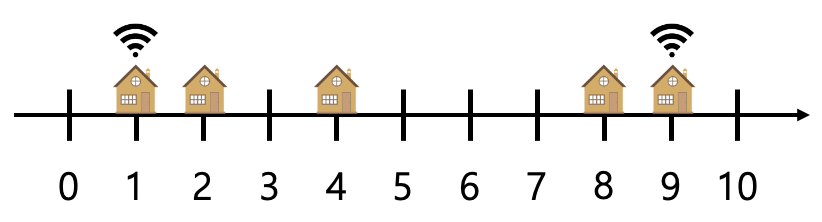
그림 1. 최대 거리 배치

이러한 경우 거리는 8 입니다. 근데.. 저희는 또하나 따져야할 조건이 있었죠.

바로 설치해야하는 공유기 개수입니다.

 

예제는 3개를 설치하라 했으니, 아래처럼 하면 문제 조건에 맞습니다. (물론 9대신 8에 공유기를 설치해도 됩니다.)

그림 2. 문제 결과

결과는 4 - 1 = 3 이 나옵니다.

직관적으로 봤을때, 이 예제는 데이터 수가 적으니 대충 조합으로 다 돌려봐도 찾을 수 있겠죠.

하지만, 주어진 범위에서 조합을 돌리면 최대 20만개 중에 10만개의 경우를 고려해야합니다.

 

조금 다르게 생각해볼게요.

가장 인접한 공유기의 설치 가능 거리: WiFi_d

설치할 수 있는 공유기의 수: WiFi_c

WiFi_d가 줄어들수록 WiFi_c는 동일하거나 더 늘어나겠죠?

 

 

위의 예제로 생각해보면 아래와 같은 데이터를 얻을 수 있습니다.

WiFi_d == 1, WiFi_c == 5
WiFi_d == 2, WiFi_c == 3
WiFi_d == 3, WiFi_c == 3 ....

 

일반화해서 그래프로 그리면, 1차 함수 형태가 나올 것 같습니다. 단조 감소하는 형태죠.

WiFi_d가 계속 커지는 상황에서 WiFi_c가 갑자기 커지는 상황은 올 수 없을테니까요.

아 물론 한집에 여러개 설치했다가 뺐다가.. x병 떨면 가능한데, 문제 조건에서 미리 막아줬네요 ㅎㅎ

그림 3. WiFi_d :: WiFi_c 상관 그래프

 

단조 감소/증가에 사용될 수 있는 알고리즘, '이분탐색' 기억나시나요?

특히, d의 값 입력이 10억까지 들어오기 때문에... 점차 확신이 듭니다. ㅎㅎ

 

 

풀이

이제부터 우리는 WiFi_d 값을 이분탐색으로 돌리고, 그때 설치할 수 있는 최대 WiFi_c의 값을 찾을겁니다.

여기서 최대 WiFi_c를 찾는다는 이야기는 신호에 벗어나는 집이라면 무조건 공유기를 설치한다는 의미와 같습니다.

와우.. 상당히 greeeeeedy 하져?

 

이 문제를 그리디하게 풀어도 되는 이유는 뭘까요. 여러가지 조건을 생각해봅시다.

그림 4. 그리디 파악

위와 같은 구성에서 생각해보겠습니다. (단, x > y)

 

WiFi 공유기가 닿을 수 있는 범위를 distance로 정의하고, 각 집 사이의 거리를 x, y로 표기하겠습니다.

그리고, 특정 distance(target) 값을 기준으로 탐색하기 때문에 범위에 포함되는 경우 공유기를 설치하지 않습니다.

i) distance > x + y 인 경우

x, x + y 위치에 모두 공유기를 설치하지 않습니다.

ii) x < distance <= x + y 인 경우

우선 x엔 공유기 설치를 뛰어넘고. 이후 x + y만큼 떨어진 집에 공유기를 설치합니다. (신호가 닿지 않기 때문에)

iii) distance < y 인 경우

가는 곳 마다 wifi를 설치할 수 있습니다.

 

ii)와 i) 그리고 iii)와 ii), i)을 비교해 봤을 때, 각 조건이 상위 조건의 부분 집합이 되는 것을 볼 수 있습니다.

그리디의 정의에 부합하네요.

 

또한, 그리디하게 공유기를 무작정 설치한 경우 공유기가 C개 설치되었을 때 최적값을 찾을 순 있을까요?

이게 무슨 개소리지??

예를 들어 위의 입력 예제처럼 집이 5채 일 때 공유기 3개를 채우는 경우는 위와 같이 3이 나와야합니다.

즉, 3의 간격을 타겟으로 삼은 경운데 이러한 경우 그리디하게 1은 무조건 설치하고 이후엔 4, 8에 설치해서 3개가 될 겁니다.

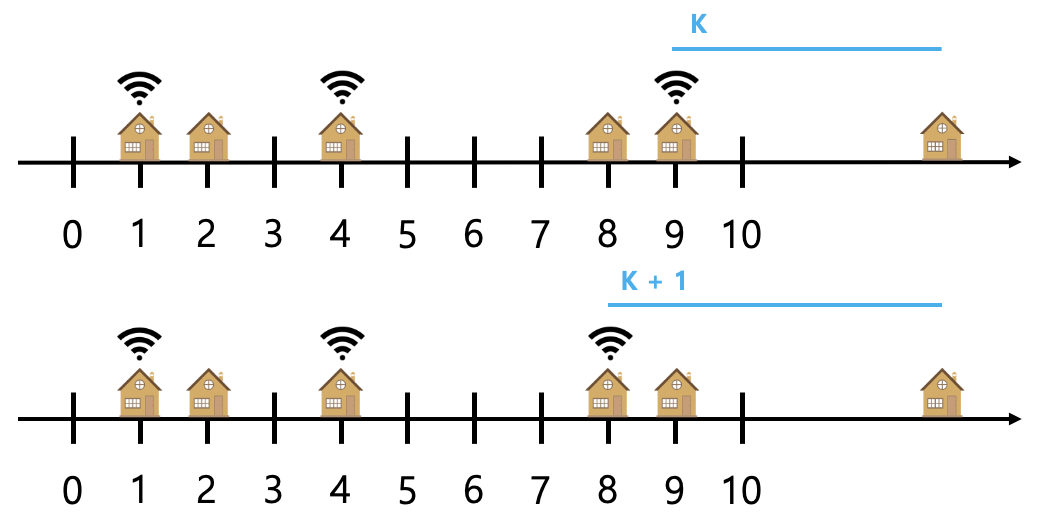
그림 5. 신호가 닿지 않는 가까운 곳에 설치해도 가능한가?

신호가 닿지 않는 가장 가까운 곳에 설치한다는 것은 일반화하면 위와 같은 차이를 보여줍니다.

즉, 오히려 떨어진 거리는 더 멀어지게됩니다.

따라서 그리디한 선택이 계속해서 더 넓은 간격을 만들고 결국, C개를 설치를 완료할 때까지 이보다 더 나은 결과를 제공하진 못합니다.

 

 

코드

이렇게 증명은 완료되었습니다. 말한 그대로 코드를 구현해 볼게요.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int C = Integer.parseInt(st.nextToken());

        int[] router = new int[N];
        for(int i = 0; i < N; i++) {
            router[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(router);
        System.out.println(binarySearch(router, C));
    }

    private static int binarySearch(int[] arr, int hits) {
        int start = 0, end = arr[arr.length - 1];
        int res = 0;

        while(start <= end) {
            int mid = (start + end) >> 1;
            int count = getCount(mid, arr);

            if(hits <= count) {
                start = mid + 1;
                res = mid;
            }
            else {
                end = mid - 1;
            }
        }

        return res;
    }

    private static int getCount(int target, int[] arr) {
        int count = 1;
        int settingAP = arr[0];

        for(int i = 1; i < arr.length; i++) {
            if(target > arr[i] - settingAP) continue;
            count++;
            settingAP = arr[i];
        }

        return count;
    }
}

getCount 메서드에서 간격을 측정하고 공유기 설치 여부를 결정합니다.

위에서 설명은 다했으니 여기서 마무리 짓겠습니다.

여기까지 오느라 고생하셨습니다.. 아 물론 저도요 ㅎㅎ

 

시간 복잡도는 집의 좌표(X_N)가 10억까지니까, 대략 O(NlogX_N) = 20만 * log10억 = 20만 * 30 = 600만 정도 나옵니다.

 

 

 

설명이 부족한 부분이나, 틀린 부분 있으면 댓글 달아주세요!

빠르게 답변이나 보완하도록 하겠습니다. 감사합니다.